题目内容
(满分12分)设f (x) 是定义在 [-1,1] 上的偶函数,f (x) 与g(x) 的图象关于x =" 1" 对称,且当x Î [2,3] 时,g(x) = a (x-2)-2 (x-2) 3(a 为常数).
 (Ⅰ)求f (x) 的解析式;
(Ⅰ)求f (x) 的解析式;
(Ⅱ)若f (x) 在 [0,1] 上是增函数,求实数a 的取值范围;
(Ⅲ)若a Î (-6,6),问能否使f (x) 的最大值为 4?请说明理由.
Î (-6,6),问能否使f (x) 的最大值为 4?请说明理由.
 (Ⅰ)求f (x) 的解析式;
(Ⅰ)求f (x) 的解析式;(Ⅱ)若f (x) 在 [0,1] 上是增函数,求实数a 的取值范围;
(Ⅲ)若a
 Î (-6,6),问能否使f (x) 的最大值为 4?请说明理由.
Î (-6,6),问能否使f (x) 的最大值为 4?请说明理由.(Ⅰ) f (x) =
(Ⅱ) a≥6,即aÎ [6,+¥)
(Ⅲ)当aÎ (-6,6) 时,f (x) 的最大值不可能为 4
(Ⅱ) a≥6,即aÎ [6,+¥)
(Ⅲ)当aÎ (-6,6) 时,f (x) 的最大值不可能为 4
(I) ∵ f (x) 与g(x) 的图象关于直线x =" 1" 对称,
∴ f (x) = g(2-x) . 1分
∴ 当xÎ [-1,0] 时,2-xÎ [2,3],
∴ f (x) = g(2-x) = -ax + 2x 3 . 2分
又∵ f (x) 为偶函数,
∴ xÎ [0,1] 时,-xÎ [-1,0],
∴ f (x) = f (-x) = ax-2x 3. 3分
∴ f (x) = . 4分
(II) ∵ f (x) 为 [0,1] 上的增函数,
∴ f’(x) = a-6x 2≥0 Þa≥6x 2 在区间 [0,1] 上恒成立. 6分
∵ xÎ [0,1] 时,6x 2≤6 , 7分
∴ a≥6,即aÎ [6,+¥) . 8分
(III) 由f (x) 为偶函数,故只需考虑xÎ [0,1],
由f’(x) =" 0" 得x = , 9分
由f () =" 4" Þa =" 6" , 10分
此时x = 1, 11分
当aÎ (-6,6) 时,f (x) 的最大值不可能为 4 . 12分
∴ f (x) = g(2-x) . 1分
∴ 当xÎ [-1,0] 时,2-xÎ [2,3],
∴ f (x) = g(2-x) = -ax + 2x 3 . 2分
又∵ f (x) 为偶函数,
∴ xÎ [0,1] 时,-xÎ [-1,0],
∴ f (x) = f (-x) = ax-2x 3. 3分
∴ f (x) = . 4分
(II) ∵ f (x) 为 [0,1] 上的增函数,
∴ f’(x) = a-6x 2≥0 Þa≥6x 2 在区间 [0,1] 上恒成立. 6分
∵ xÎ [0,1] 时,6x 2≤6 , 7分
∴ a≥6,即aÎ [6,+¥) . 8分
(III) 由f (x) 为偶函数,故只需考虑xÎ [0,1],
由f’(x) =" 0" 得x = , 9分
由f () =" 4" Þa =" 6" , 10分
此时x = 1, 11分
当aÎ (-6,6) 时,f (x) 的最大值不可能为 4 . 12分

练习册系列答案
相关题目


 我们知道:人们对声音有不同的感觉,这与它的强度有关系,声音的强度用
我们知道:人们对声音有不同的感觉,这与它的强度有关系,声音的强度用 (单位:
(单位: )表示,但在实际测量时,常用声音的强度水平
)表示,但在实际测量时,常用声音的强度水平 (单位:分贝)表示,它们满足公式: (
(单位:分贝)表示,它们满足公式: ( ,其中
,其中 (
( 是人们能听到的最小强度,是听觉的开始.请回答以下问题:
是人们能听到的最小强度,是听觉的开始.请回答以下问题: (
( (
( (
( 的声音的强度水平必须保持在
的声音的强度水平必须保持在 分贝以下(不含
分贝以下(不含 其中实
其中实 数
数 。
。 的单调区间;
的单调区间; 与
与 的图象只有一个公共点时,记
的图象只有一个公共点时,记 的最小值为
的最小值为 ,求
,求 内均
内均 为增函数,求
为增函数,求 的取值范围
的取值范围
 =2(x>0,y>0),则xy的最小值是( )
=2(x>0,y>0),则xy的最小值是( )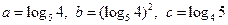 ,则( )
,则( )

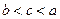


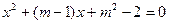 的两个实根一个小于
的两个实根一个小于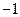 ,另一个大于
,另一个大于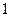 ,那么实数
,那么实数 的取值范围是
的取值范围是 。
。 (其中
(其中 是自然对数的底数,
是自然对数的底数, )根的描述正确的是( )
)根的描述正确的是( ) ,方程
,方程