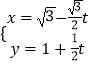题目内容
【题目】已知x,y∈R.
(Ⅰ)若x,y满足 ![]() ,
, ![]() ,求证:
,求证: ![]() ;
;
(Ⅱ)求证:x4+16y4≥2x3y+8xy3 .
【答案】证明:(Ⅰ)利用绝对值不等式的性质得: |x|= ![]() [|2(x﹣3y)+3(x+2y)|]≤
[|2(x﹣3y)+3(x+2y)|]≤ ![]() [|2(x﹣3y)|+|3(x+2y)|]<
[|2(x﹣3y)|+|3(x+2y)|]< ![]() (2×
(2× ![]() +3×
+3× ![]() )=
)= ![]() ;
;
(Ⅱ)因为x4+16y4﹣(2x3y+8xy3)=x4﹣2x3y+16y4﹣8xy3=x3(x﹣2y)+8y3(2y﹣x)
=(x﹣2y)(x3﹣8y3)=(x﹣2y)(x﹣2y)(x2+2xy+4y2)
=(x﹣2y)2[(x+y)2+3y2]≥0,
∴x4+16y4≥2x3y+8xy3
【解析】(Ⅰ)|x|= ![]() [|2(x﹣3y)+3(x+2y)|]≤
[|2(x﹣3y)+3(x+2y)|]≤ ![]() [|2(x﹣3y)|+|3(x+2y)|]<
[|2(x﹣3y)|+|3(x+2y)|]< ![]() (2×
(2× ![]() +3×
+3× ![]() )=
)= ![]() ;(Ⅱ)x4+16y4﹣(2x3y+8xy3)=x4﹣2x3y+16y4﹣8xy3=x3(x﹣2y)+8y3(2y﹣x)=(x﹣2y)2[(x+y)2+3y2]≥0即可
;(Ⅱ)x4+16y4﹣(2x3y+8xy3)=x4﹣2x3y+16y4﹣8xy3=x3(x﹣2y)+8y3(2y﹣x)=(x﹣2y)2[(x+y)2+3y2]≥0即可
【考点精析】解答此题的关键在于理解不等式的证明的相关知识,掌握不等式证明的几种常用方法:常用方法有:比较法(作差,作商法)、综合法、分析法;其它方法有:换元法、反证法、放缩法、构造法,函数单调性法,数学归纳法等.

练习册系列答案
相关题目