题目内容
【题目】设
是圆
上的动点，点
是在
轴上的投影，且
.
（1）当在圆上运动时，求点
的轨迹
的方程；
（2）求过点(1,0)，倾斜角为
的直线被所截线段的长度.
【答案】（1）
（2）
【解析】
（1）设
的坐标为
,
的坐标为
.由
,可得
,可列出,坐标关系式为,即可得到的轨迹
的方程.
（2）设直线方程为:
,代入椭圆方程,由韦达定理和弦长公式:
,即可求得直线被C所截线段的长度.
（1）设的坐标为,的坐标为.
由,可得,
的坐标为,是圆
上的动点
┄①
,坐标关系式为:
┄②代入①得:
整理可得的轨迹的方程:
（2）求过点
,倾斜角为
的直线方程为:
设直线与轨迹的交点为
将直线方程与轨迹方程联立方程组,消掉
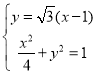得: 
整理可得:
根据韦达定理得:
∴线段AB的长度为:
所以线段AB的长度:.
【题目】党的十九大报告中多次出现的“绿色”“低碳”“节约”等词语，正在走入百姓生活，绿色出行的理念已深入人心，骑自行车或步行渐渐成为市民的一种出行习惯.某市环保机构随机抽查统计了该市1800名成年市民某月骑车次数在各区间的人数，统计如下表：
次数 年龄 | [0，10） | [10，20） | [20，30） | [30，40） | [40，50） | [50，60） |
18岁至31岁 | 8 | 12 | 20 | 60 | 140 | 150 |
32岁至44岁 | 12 | 28 | 20 | 140 | 60 | 150 |
45岁至59岁 | 25 | 50 | 80 | 100 | 225 | 450 |
60岁及以上 | 25 | 10 | 10 | 19 | 4 | 2 |
联合国世界卫生组织于2013年确定新的年龄分段：44岁及以下为青年人，45岁至59岁为中年人，60岁及以上为老人.
（1）若从被抽查的该月骑车次数在
的老年人中随机选出两名幸运者给予奖励，求其中一名幸运者该月骑车次数在
之间，另一名幸运者该月骑车次数在
之间概率；
（2）若月骑车次数不少于30次者被称为“骑行爱好者”，将上面提供的数据进行统计后，把答卷中的
列联表补充完整，并计算说明能否在犯错误不超过0.001的前提下认为“骑行爱好者”与“青年人”有关？
参考数据：
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
，其中
