题目内容
(14分)
设集合W由满足下列两个条件的数列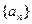 构成:
构成:
①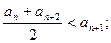
②存在实数M,使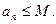 (n为正整数)
(n为正整数)
(I)在只有5项的有限数列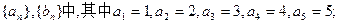
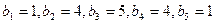 ;试判断数列
;试判断数列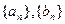 是否为集合W的元素;
是否为集合W的元素;
(II)设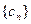 是等差数列,
是等差数列,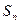 是其前n项和,
是其前n项和,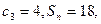 证明数列
证明数列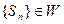 ;并写出M的取值范围;
;并写出M的取值范围;
(III)设数列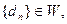 且对满足条件的常数M,存在正整数k,使
且对满足条件的常数M,存在正整数k,使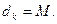
求证: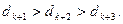
设集合W由满足下列两个条件的数列
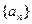 构成:
构成:①
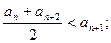
②存在实数M,使
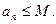 (n为正整数)
(n为正整数)(I)在只有5项的有限数列
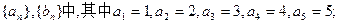
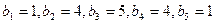 ;试判断数列
;试判断数列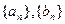 是否为集合W的元素;
是否为集合W的元素;(II)设
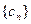 是等差数列,
是等差数列,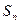 是其前n项和,
是其前n项和,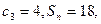 证明数列
证明数列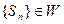 ;并写出M的取值范围;
;并写出M的取值范围;(III)设数列
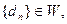 且对满足条件的常数M,存在正整数k,使
且对满足条件的常数M,存在正整数k,使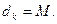
求证:
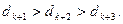
(I)对于数列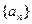 ,当n=1时,
,当n=1时,
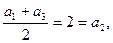 显然不满足集合W的条件,①
显然不满足集合W的条件,①
故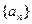 不是集合W中的元素, …………2分
不是集合W中的元素, …………2分
对于数列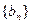 ,当
,当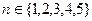 时,
时,
不仅有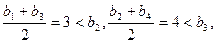
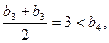 而且有
而且有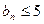 ,
,
显然满足集合W的条件①②,
故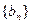 是集合W中的元素. …………4分
是集合W中的元素. …………4分
(II)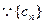 是等差数列,
是等差数列,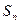 是其前n项和,
是其前n项和,
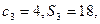 设其公差为d,
设其公差为d,
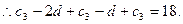
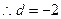
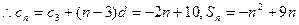 …………7分
…………7分

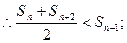
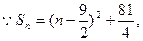
 的最大值是
的最大值是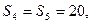
即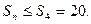
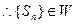 ,且M的取值范围是
,且M的取值范围是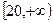 …………9分
…………9分
(III)证明: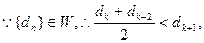
整理 ,
,
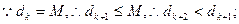
又
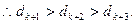 …………14分
…………14分
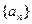 ,当n=1时,
,当n=1时,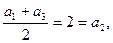 显然不满足集合W的条件,①
显然不满足集合W的条件,①故
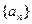 不是集合W中的元素, …………2分
不是集合W中的元素, …………2分对于数列
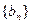 ,当
,当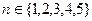 时,
时,不仅有
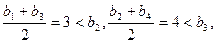
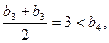 而且有
而且有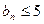 ,
,显然满足集合W的条件①②,
故
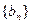 是集合W中的元素. …………4分
是集合W中的元素. …………4分(II)
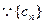 是等差数列,
是等差数列,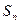 是其前n项和,
是其前n项和,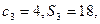 设其公差为d,
设其公差为d,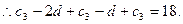
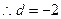
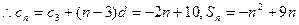 …………7分
…………7分
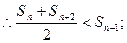
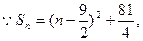
 的最大值是
的最大值是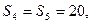
即
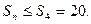
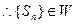 ,且M的取值范围是
,且M的取值范围是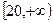 …………9分
…………9分(III)证明:
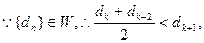
整理
 ,
,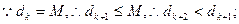
又

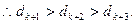 …………14分
…………14分略

练习册系列答案
相关题目
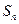 是数列
是数列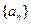 (
(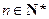 )的前
)的前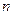 项和,
项和,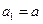 ,且
,且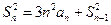 ,
,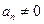 ,
,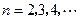 .
.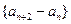 (
(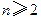 )是常数数列;
)是常数数列;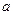 ,使以18为首项,7为公比的等比数列
,使以18为首项,7为公比的等比数列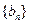 (
(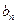 是数列
是数列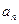 }是整数组成的数列,a1 = 1,且点
}是整数组成的数列,a1 = 1,且点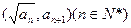 在函数
在函数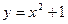 的图象上,
的图象上,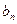 }满足
}满足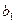 = 1,
= 1,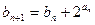 ,求证:
,求证: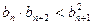
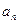 }的前n项和为
}的前n项和为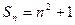 ,则 ( )
,则 ( )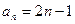
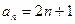

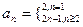
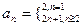
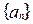 ,
,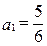 ,若以
,若以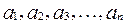 为系数的二次方程
为系数的二次方程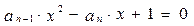 都有根
都有根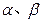 ,且满足
,且满足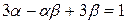 。
。 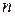 项和
项和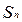 .
.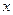 ,以后每次生成的结果可将上一次生成的每一个数
,以后每次生成的结果可将上一次生成的每一个数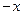 ,另一个是
,另一个是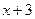 .设第
.设第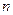 次生成的数的个数为
次生成的数的个数为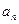 ,则数列
,则数列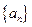 的前
的前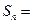 _________________;若
_________________;若 ,前
,前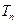 ,则
,则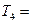 ______________________.
______________________.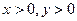 ,且
,且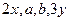 成等差数列,
成等差数列,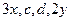 成等比数列,则
成等比数列,则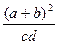 的最小值为 ( )
的最小值为 ( )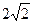
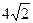
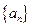 中,
中,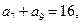
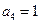 ,则
,则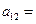
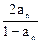 , 则a 5 =
, 则a 5 =