题目内容
设双曲线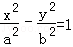 的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为( )
的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为( )
A. | B.5 | C.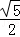 | D.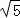 |
C
解析试题分析:将双曲线的渐进线方程 代如抛物线方程y=x2+1中化简得
代如抛物线方程y=x2+1中化简得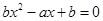 ,由只有一公共点可知
,由只有一公共点可知 即
即 ,所以
,所以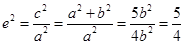 即
即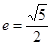 ,答案选C.
,答案选C.
考点:1.双曲线的渐进线方程;2.直线与抛物线的位置关系

练习册系列答案
相关题目
设 是椭圆
是椭圆 的左、右焦点,
的左、右焦点, 为直线
为直线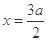 上一点,
上一点,
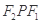 是底角为
是底角为 的等腰三角形,则
的等腰三角形,则 的离心率为( )
的离心率为( )
A. | B. | C. | D. |
已知 是抛物线
是抛物线 上任意一点,则当
上任意一点,则当 点到直线
点到直线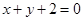 的距离最小时,
的距离最小时, 点与该抛物线的准线的距离是
点与该抛物线的准线的距离是
| A.2 | B.1 | C. | D. |
设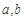 是关于t的方程
是关于t的方程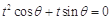 的两个不等实根,则过
的两个不等实根,则过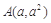 ,
,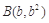 两点的直线与双曲线
两点的直线与双曲线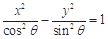 的公共点的个数为
的公共点的个数为
| A.3 | B.2 | C.1 | D.0 |
(本小题满分12分)
已知椭圆C1和抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为原点,从它们每条曲线 上至少取两个点,将其坐标记录于下表中:
上至少取两个点,将其坐标记录于下表中:
| x | 5 | - | 4 |  |  |
| y | 2 | 0 | -4 |  | - |

(Ⅰ)求C1和C2的方程;
(Ⅱ)过点S(0,-
 )且斜率为k的动直线l交椭圆C1于A、B两点,在y轴上是否存在定点D,使以线段AB为直径的圆恒过这个点?若存在,求出D的坐标,若不存在,说明理由.
)且斜率为k的动直线l交椭圆C1于A、B两点,在y轴上是否存在定点D,使以线段AB为直径的圆恒过这个点?若存在,求出D的坐标,若不存在,说明理由. 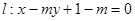
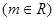 ,圆
,圆 .
.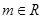 ,直线
,直线 与圆
与圆 恒有两个公共点.
恒有两个公共点.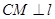 于点
于点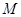 ,当
,当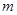 变化时,求点
变化时,求点 的方程.
的方程.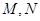 ,与圆
,与圆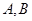 ,是否存在
,是否存在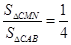 ?若存在,试求出
?若存在,试求出 的圆心为
的圆心为 ,圆
,圆 :
: 的圆心为
的圆心为 的轨迹方程;
的轨迹方程;  ,使得
,使得 为钝角?若存在,求出点
为钝角?若存在,求出点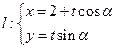 (
(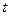 为参数),圆
为参数),圆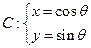 (
( 为参数).
为参数).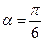 时,试判断直线
时,试判断直线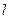 与圆
与圆 的位置关系;
的位置关系; ,则C的实轴长为( )
,则C的实轴长为( )