题目内容
(本题满分12分)已知函数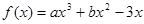 在
在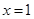 处取得极值-2.
处取得极值-2.
(1)求函数 的解析式;
的解析式;
(2)求曲线 在点
在点 处的切线方程.
处的切线方程.
(1)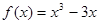 ;(2)
;(2)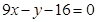 .
.
解析试题分析:(1)先对函数 求导,在取得极值处导数值为0,则
求导,在取得极值处导数值为0,则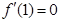 ,又极值为
,又极值为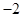 ,可得
,可得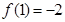 ,可得关于
,可得关于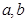 的方程,解得
的方程,解得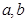 可知解析式;(2)由(1)可得
可知解析式;(2)由(1)可得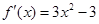 ,在
,在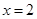 处的切线的斜率为
处的切线的斜率为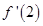 ,过切点
,过切点 ,由直线方程的点斜式,写出切线方程.
,由直线方程的点斜式,写出切线方程.
解:(1)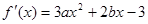 , 1分
, 1分
依题意有,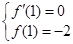 ,即
,即 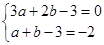 , 3分
, 3分
解得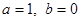 , 5分
, 5分
∴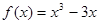 . 6分
. 6分
(2)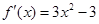 ,
,
∴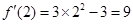 ,又
,又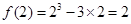 , 9分
, 9分
故曲线 在点
在点 处的切线方程为
处的切线方程为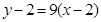 ,
,
即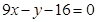 12分
12分
考点:求函数的极值,求曲线的切线方程.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 .
. 时,求
时,求 的极值;
的极值; 上单调递增,求b的取值范围.
上单调递增,求b的取值范围. 。
。 时,①求函数
时,①求函数 的单调区间;②求函数
的单调区间;②求函数 处的切线方程;
处的切线方程; 既有极大值,又有极小值,且当
既有极大值,又有极小值,且当 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围. ,当
,当 时,有极大值
时,有极大值 .
.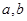 的值;
的值; 的极小值.
的极小值.
 ,函数
,函数
 时,求函数
时,求函数 的表达式;
的表达式; ,函数
,函数 上的最小值是2 ,求
上的最小值是2 ,求 的值;
的值; 与函数
与函数 ,它们的定义域都是(0,e],其中e是自然对数的底e≈2.7,a∈R.
,它们的定义域都是(0,e],其中e是自然对数的底e≈2.7,a∈R. 对一切m,n∈(0,e]恒成立;
对一切m,n∈(0,e]恒成立; 元,并且每件产品需向总公司交
元,并且每件产品需向总公司交 元(
元( )时,一年的销售量为
)时,一年的销售量为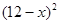 万件.
万件. (万元)与每件产品的售价
(万元)与每件产品的售价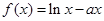 ,
, 为常数.
为常数.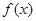 在
在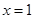 处的切线与
处的切线与 轴平行,求
轴平行,求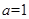 时,试比较
时,试比较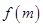 与
与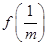 的大小;
的大小;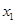 、
、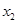 ,试证明
,试证明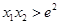 .
.