题目内容
(本题满分16分)设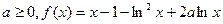 ,
,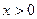
(1)令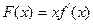 ,讨论
,讨论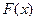 在(0.+∞)内的单调性并求极值;
在(0.+∞)内的单调性并求极值;
(2)求证:当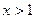 时,恒有
时,恒有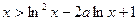 。
。
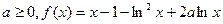 ,
,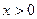
(1)令
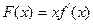 ,讨论
,讨论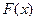 在(0.+∞)内的单调性并求极值;
在(0.+∞)内的单调性并求极值;(2)求证:当
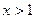 时,恒有
时,恒有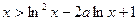 。
。(1)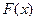 在
在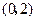 内是减函数,在
内是减函数,在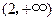 内是增函数,
内是增函数, 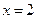 处取得极小值
处取得极小值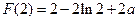 (2)同解析.
(2)同解析.
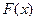 在
在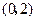 内是减函数,在
内是减函数,在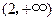 内是增函数,
内是增函数, 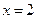 处取得极小值
处取得极小值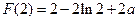 (2)同解析.
(2)同解析. (1)根据求导法则有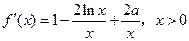 , ………………………2分
, ………………………2分
故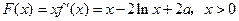 ,
,
于是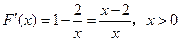 , ……………………4分
, ……………………4分
列表如下:
故知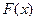 在
在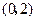 内是减函数,在
内是减函数,在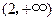 内是增函数,所以在
内是增函数,所以在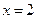 处取得极小值
处取得极小值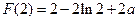 . ………………………8分
. ………………………8分
(Ⅱ)证明:由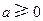 知,
知,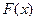 的极小值
的极小值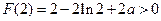 .
.
于是由上表知,对一切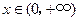 ,恒有
,恒有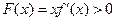 . ………………………10分
. ………………………10分
从而当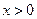 时,恒有
时,恒有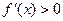 ,故
,故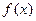 在
在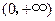 内单调增加. …………………12分
内单调增加. …………………12分
所以当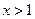 时,
时,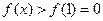 ,即
,即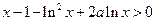 .
.
故当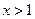 时,恒有
时,恒有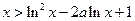 . …………………16分
. …………………16分
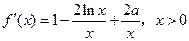 , ………………………2分
, ………………………2分故
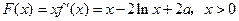 ,
,于是
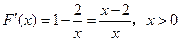 , ……………………4分
, ……………………4分列表如下:
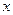 | 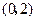 | 2 | 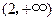 |
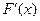 | 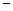 | 0 | 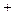 |
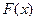 | 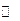 | 极小值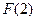 |  |
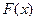 在
在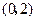 内是减函数,在
内是减函数,在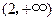 内是增函数,所以在
内是增函数,所以在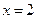 处取得极小值
处取得极小值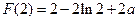 . ………………………8分
. ………………………8分(Ⅱ)证明:由
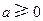 知,
知,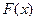 的极小值
的极小值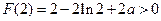 .
.于是由上表知,对一切
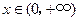 ,恒有
,恒有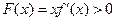 . ………………………10分
. ………………………10分从而当
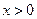 时,恒有
时,恒有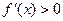 ,故
,故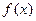 在
在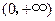 内单调增加. …………………12分
内单调增加. …………………12分所以当
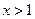 时,
时,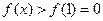 ,即
,即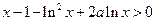 .
.故当
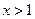 时,恒有
时,恒有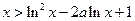 . …………………16分
. …………………16分
练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
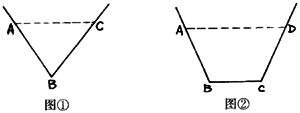
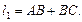
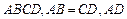 ∥
∥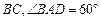 ,过水湿周
,过水湿周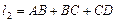 .若
.若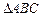 与梯形ABCD的面积都为S,
与梯形ABCD的面积都为S,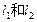 的最小值;
的最小值;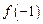 的值,使函数
的值,使函数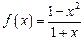 在点
在点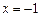 处连续,则
处连续,则

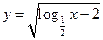 的定义域为 .
的定义域为 .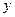 轴对称;
轴对称;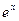 ,则
,则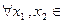
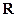 ,都有
,都有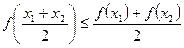 ;
;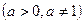 在(0,+∞)上单调递增,则f(-2)> f(a+1);
在(0,+∞)上单调递增,则f(-2)> f(a+1);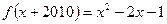 (x∈
(x∈ 序号是 .
序号是 . 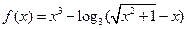 ,则对于任意实数
,则对于任意实数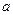 、
、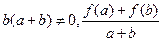 的值
的值 )f′(x)<0 ,
)f′(x)<0 , 若x1<x2,且x1+x2>3则有 ( )
若x1<x2,且x1+x2>3则有 ( )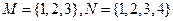 ,定义函数
,定义函数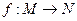 。若点
。若点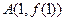 、
、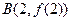 、
、 ,
,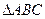 的外接圆圆心为
的外接圆圆心为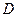 ,且
,且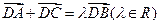 ,则满足条件的函数
,则满足条件的函数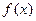 有( )
有( )