题目内容
已知抛物线y2=2px(p>0)上一点M(1,m)(m>0)到其焦点的距离为5,双曲线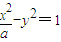 的左顶点为A,若双曲线的一条渐近线与直线AM平行,则实数a的值是( )
的左顶点为A,若双曲线的一条渐近线与直线AM平行,则实数a的值是( )A.
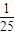
B.

C.
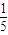
D.

【答案】分析:根据抛物线的定义,可得点M到抛物线的准线x=-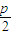 的距离也为5,即即|1+
的距离也为5,即即|1+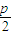 |=5,解可得p=8,可得抛物线的方程,进而可得M的坐标;根据双曲线的性质,可得A的坐标与其渐近线的方程,根据题意,双曲线的一条渐近线与直线AM平行,可得
|=5,解可得p=8,可得抛物线的方程,进而可得M的坐标;根据双曲线的性质,可得A的坐标与其渐近线的方程,根据题意,双曲线的一条渐近线与直线AM平行,可得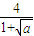 =
=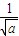 ,解可得a的值,即可得答案.
,解可得a的值,即可得答案.
解答:解:根据题意,抛物线y2=2px(p>0)上一点M(1,m)(m>0)到其焦点的距离为5,则点M到抛物线的准线x=-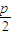 的距离也为5,
的距离也为5,
即|1+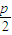 |=5,解可得p=8;即抛物线的方程为y2=16x,
|=5,解可得p=8;即抛物线的方程为y2=16x,
易得m2=2×8=16,则m=4,即M的坐标为(1,4)
双曲线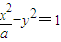 的左顶点为A,则a>0,且A的坐标为(-
的左顶点为A,则a>0,且A的坐标为(-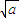 ,0),
,0),
其渐近线方程为y=±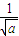 x;
x;
而KAM=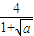 ,
,
又由若双曲线的一条渐近线与直线AM平行,则有 =
=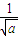 ,
,
解可得a= ;
;
故选B.
点评:本题综合考查双曲线与抛物线的性质,难度一般;需要牢记双曲线的渐近线方程、定点坐标等.
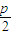 的距离也为5,即即|1+
的距离也为5,即即|1+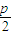 |=5,解可得p=8,可得抛物线的方程,进而可得M的坐标;根据双曲线的性质,可得A的坐标与其渐近线的方程,根据题意,双曲线的一条渐近线与直线AM平行,可得
|=5,解可得p=8,可得抛物线的方程,进而可得M的坐标;根据双曲线的性质,可得A的坐标与其渐近线的方程,根据题意,双曲线的一条渐近线与直线AM平行,可得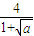 =
=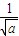 ,解可得a的值,即可得答案.
,解可得a的值,即可得答案.解答:解:根据题意,抛物线y2=2px(p>0)上一点M(1,m)(m>0)到其焦点的距离为5,则点M到抛物线的准线x=-
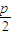 的距离也为5,
的距离也为5,即|1+
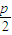 |=5,解可得p=8;即抛物线的方程为y2=16x,
|=5,解可得p=8;即抛物线的方程为y2=16x,易得m2=2×8=16,则m=4,即M的坐标为(1,4)
双曲线
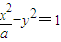 的左顶点为A,则a>0,且A的坐标为(-
的左顶点为A,则a>0,且A的坐标为(-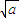 ,0),
,0),其渐近线方程为y=±
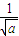 x;
x;而KAM=
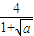 ,
,又由若双曲线的一条渐近线与直线AM平行,则有
 =
=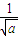 ,
,解可得a=
 ;
;故选B.
点评:本题综合考查双曲线与抛物线的性质,难度一般;需要牢记双曲线的渐近线方程、定点坐标等.

练习册系列答案
相关题目