题目内容
在数列{an}中,已知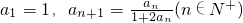 .
.
(1)求a2,a3,a4,并由此猜想数列{an}的通项公式an的表达式;
(2)用适当的方法证明你的猜想.
解:(1)∵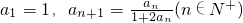 .
.
∴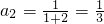 ….(1分)
….(1分)
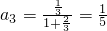 …(2分)
…(2分)
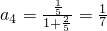 …(3分)
…(3分)
由此猜想数列{an}的通项公式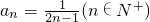 …..(5分)
…..(5分)
(2)下面用数学归纳法证明
①当n=1时,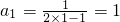 ,猜想成立…..(6分)
,猜想成立…..(6分)
②假设当n=k(k∈N+,k≥1)猜想成立,即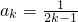 ….(7分)
….(7分)
∵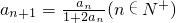 .…(8分)
.…(8分)
∴ …(12分)
…(12分)
即当n=k+1时猜想也成立…..(13分)
根据①和②,可知猜想对任何n∈N+都成立…..(14分)
(用其他方法正确证明也给分)
分析:(1)利用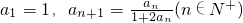 ,n分别取2,3,4,可求出a2,a3,a4,并由此猜想数列{an}的通项公式;
,n分别取2,3,4,可求出a2,a3,a4,并由此猜想数列{an}的通项公式;
(2)用数学归纳法证明:①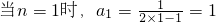 ,猜想成立;②假设当n=k时成立,利用
,猜想成立;②假设当n=k时成立,利用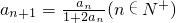 ,可证得当n=k+1时猜想也成立,故可得结论.
,可证得当n=k+1时猜想也成立,故可得结论.
点评:本题以数列递推式为载体,考查数列的通项的猜想与证明,解题的关键是利用数学归纳法证明,尤其第二步的证明.
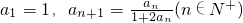 .
.∴
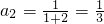 ….(1分)
….(1分)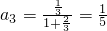 …(2分)
…(2分)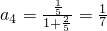 …(3分)
…(3分)由此猜想数列{an}的通项公式
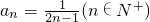 …..(5分)
…..(5分)(2)下面用数学归纳法证明
①当n=1时,
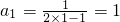 ,猜想成立…..(6分)
,猜想成立…..(6分)②假设当n=k(k∈N+,k≥1)猜想成立,即
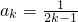 ….(7分)
….(7分)∵
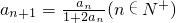 .…(8分)
.…(8分)∴
 …(12分)
…(12分)即当n=k+1时猜想也成立…..(13分)
根据①和②,可知猜想对任何n∈N+都成立…..(14分)
(用其他方法正确证明也给分)
分析:(1)利用
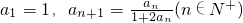 ,n分别取2,3,4,可求出a2,a3,a4,并由此猜想数列{an}的通项公式;
,n分别取2,3,4,可求出a2,a3,a4,并由此猜想数列{an}的通项公式;(2)用数学归纳法证明:①
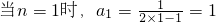 ,猜想成立;②假设当n=k时成立,利用
,猜想成立;②假设当n=k时成立,利用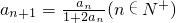 ,可证得当n=k+1时猜想也成立,故可得结论.
,可证得当n=k+1时猜想也成立,故可得结论.点评:本题以数列递推式为载体,考查数列的通项的猜想与证明,解题的关键是利用数学归纳法证明,尤其第二步的证明.

练习册系列答案
相关题目