题目内容
已知集合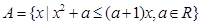 .
.
⑴是否存在实数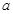 ,使得集合
,使得集合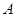 中所有整数的元素和为28?若存在,求出
中所有整数的元素和为28?若存在,求出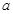 ,若不存在,请说明理由;
,若不存在,请说明理由;
⑵以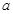 为首项,
为首项,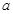 为公比的等比数列前
为公比的等比数列前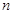 项和记为
项和记为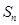 ,对任意
,对任意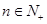 ,均有
,均有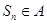 ,求
,求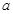 的取值范围.
的取值范围.
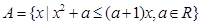 .
.⑴是否存在实数
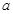 ,使得集合
,使得集合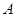 中所有整数的元素和为28?若存在,求出
中所有整数的元素和为28?若存在,求出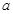 ,若不存在,请说明理由;
,若不存在,请说明理由;⑵以
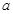 为首项,
为首项,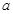 为公比的等比数列前
为公比的等比数列前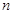 项和记为
项和记为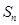 ,对任意
,对任意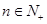 ,均有
,均有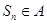 ,求
,求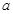 的取值范围.
的取值范围.⑴当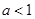 时,
时,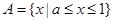 ,不符合;当
,不符合;当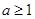 时,
时,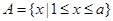 ,设
,设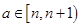 ,
,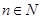 ,
,
则1+2+…+n=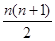 =28,所以n=7,即
=28,所以n=7,即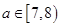
⑵ ?当
?当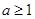 时,
时,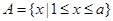 .而
.而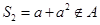 ,故
,故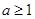 时,不存在满足条件的
时,不存在满足条件的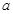 ;
;
?当 时,
时,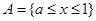 ,而
,而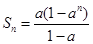 是关于
是关于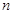 的增函数,所以
的增函数,所以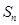 随
随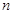 的增大而增大,
的增大而增大,
当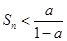 且无限接近
且无限接近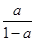 时,对任意
时,对任意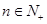 ,
,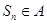 ,只须
,只须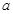 满足
满足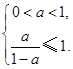 得
得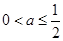 .
.
?当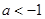 时
时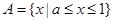 .而
.而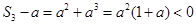 ,
,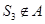 故不存在实数
故不存在实数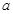 .
.
④当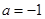 时,
时,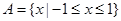 .
.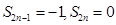 ,适合.
,适合.
⑤当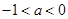 时,
时,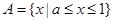 .
.
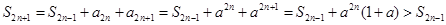 ,
,
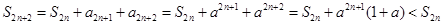 ,
,
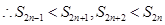 ,且
,且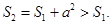
故 .
.
故只需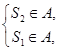 即
即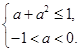 解得
解得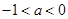 .
.
综上所述,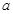 的取值范围是
的取值范围是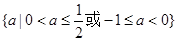 .
.
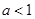 时,
时,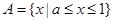 ,不符合;当
,不符合;当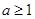 时,
时,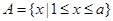 ,设
,设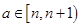 ,
,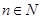 ,
,则1+2+…+n=
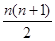 =28,所以n=7,即
=28,所以n=7,即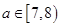
⑵
 ?当
?当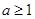 时,
时,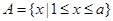 .而
.而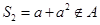 ,故
,故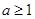 时,不存在满足条件的
时,不存在满足条件的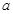 ;
;?当
 时,
时,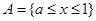 ,而
,而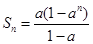 是关于
是关于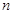 的增函数,所以
的增函数,所以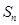 随
随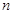 的增大而增大,
的增大而增大,当
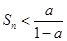 且无限接近
且无限接近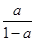 时,对任意
时,对任意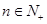 ,
,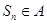 ,只须
,只须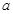 满足
满足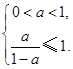 得
得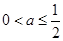 .
.?当
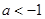 时
时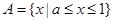 .而
.而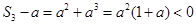 ,
,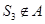 故不存在实数
故不存在实数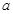 .
.④当
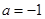 时,
时,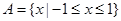 .
.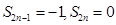 ,适合.
,适合.⑤当
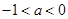 时,
时,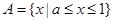 .
.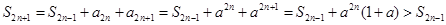 ,
,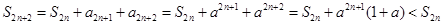 ,
,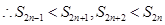 ,且
,且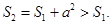
故
 .
.故只需
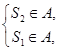 即
即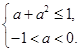 解得
解得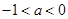 .
.综上所述,
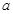 的取值范围是
的取值范围是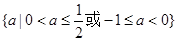 .
.略

练习册系列答案
相关题目
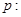 不等式
不等式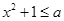 的解集为
的解集为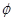 ,
,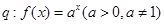 是减函数,则
是减函数,则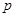 是
是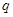 的( )
的( )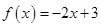 在
在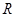 上是减函数;
上是减函数;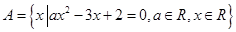 ,且
,且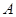 中只有一个元素,求实数
中只有一个元素,求实数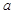 的值.
的值.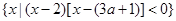 ,B=
,B=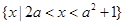 .
.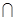 B;
B;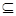 A的实数a的取值范围.
A的实数a的取值范围.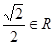 ②
②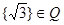 ③
③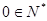 ④
④ 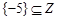
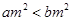 ”是“
”是“ ”的充分不必要条件
”的充分不必要条件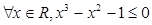 ”的否定是“
”的否定是“ 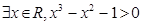 ”
”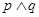 为假命题, 则
为假命题, 则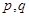 均为假命题
均为假命题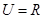 ,
,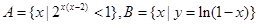 ,则右图中阴影部分表示的集合为( )
,则右图中阴影部分表示的集合为( )
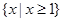
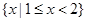
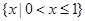

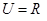 ,函数
,函数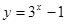 的值域为集合
的值域为集合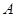 ,则
,则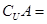
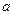 ,
,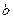 ,2},B={2,
,2},B={2,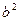 ,2
,2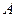 =
=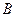 ,则
,则 .
.