题目内容

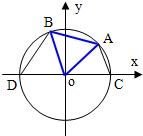精英家教网如图，A、B是单位圆O上的点，C、D分别是圆O与x轴的两个交点，△ABO为正三角形．
（1）若点A的坐标为(
3
5
，
4
5
)，求cos∠BOC的值；
（2）若∠AOC=x（0＜x＜
2π
3
），四边形CABD的周长为y，试将y表示成x的函数，并求出y的最大值．
分析：（1）根据△ABO为正三角形求得∠BOA，利用点A的坐标求得sin∠AOC和cos∠AOC，进而利用两角和公式求得cos∠BOC．
（2）利用余弦定理分别求得AC和BD，进而根据△ABO为正三角形求得AB，CD可知，四边相加得到y的函数解析式，利用两角和公式化简整理后，利用x的范围和正弦函数的性质求得函数的最大值．
解答：解：（1）∵△ABO为正三角形
∴∠BOA=60°
∵点A的坐标为(
3
5
，
4
5
)
∴tan∠AOC=
4
3
，
∴sin∠AOC=
4
5
，cos∠AOC=
3
5

∴cos∠BOC=cos（∠AOC+60°）=cos∠AOCcos60°-sin∠AOCsin60°=
3-4
3
10
；

（2）由余弦定理可知AC=
1+1-2cosx
=2sin
x
2
，BD=
1+1-2cos(π-x-
π
3
)
=2sin（
π
3
-
x
2
），
AB=OB=1，CD=2，
∴y=2sin
x
2
+2sin(
π
3
-
x
2
)+3
=2sin
x
2
+
3
cos
x
2
-sin
x
2
+3
=sin
x
2
+
3
cos
x
2
+3
=2sin(
x
2
+
π
3
)+3，0＜x＜
2π
3

∴当x=
π
3
时，ymax=5
点评：本题主要考查了三角函数的最值，数学模型的应用．考查了学生分析问题和解决问题的能力．
练习册系列答案
相关题目
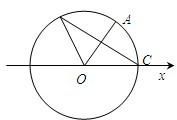精英家教网如图，A、B是单位圆O上的动点，C是圆与x轴正半轴的交点，设∠COA=α．
（1）当点A的坐标为(
3
5
，  
4
5
)时，求sinα的值；
（2）若0≤α≤
π
2
，且当点A、B在圆上沿逆时针方向移动时，总有∠AOB=
π
3
，试求BC的取值范围．
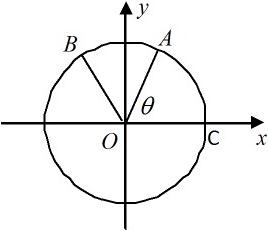精英家教网如图：A、B是单位圆上的动点，C是单位圆与x轴正半轴的交点，
且∠AOB=
π
6
，记∠COA=θ，θ∈（0，π），△AOC的面积为S．
（Ⅰ）设（θ）=OB→•OC→+2S，求f（θ）的最大值以及此时θ的值；
（Ⅱ）当A点坐标为(-
3
5
，
4
5
)时，求|
BC
|2的值．
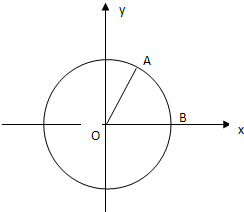如图，A，B是单位圆上的两个质点，B点坐标为（1，0），∠BOA=60°，质点A以1弧度/秒的角速度按逆时针方向在单位圆上运动；质点B以1弧度/秒的角速度按顺时针方向在单位圆上运动，过点A作AA1⊥y轴于A1，过点B作BB1⊥y轴于B1．
（1）求经过1秒后，∠BOA的弧度数；
（2）求质点A，B在单位圆上第一次相遇所用的时间；
（3）记A1B1的距离为y，请写出y与时间t的函数关系式，并求出y的最大值．
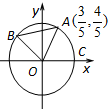如图，A、B是单位圆O上的点，C是圆O与x轴正半轴的交点，点A的坐标为(
3
5
，
4
5
)，三角形AOB为直角三角形．则cos∠COB的值是
-
4
5
-
4
5
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网