题目内容
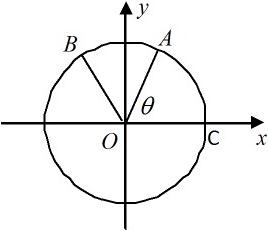 如图:A、B是单位圆上的动点,C是单位圆与x轴正半轴的交点,
如图:A、B是单位圆上的动点,C是单位圆与x轴正半轴的交点,且∠AOB=
| π |
| 6 |
(Ⅰ)设(θ)=OB→•OC→+2S,求f(θ)的最大值以及此时θ的值;
(Ⅱ)当A点坐标为(-
| 3 |
| 5 |
| 4 |
| 5 |
| BC |
分析:(1)根据三角形面积公式可知S=
sinθ,用θ分别表示出
和
,根据f(θ)=
•
+2S,θ的范围求得函数的最大值.
(2)由题意可知cosθ与sinθ,由∠BOC=θ+
,根据余弦定理即可求得答案.
| 1 |
| 2 |
| OB |
| OC |
| OB |
| OC |
(2)由题意可知cosθ与sinθ,由∠BOC=θ+
| π |
| 6 |
解答:解:(1)根据三角形面积公式可知S=
sinθ,
=(cos(θ+
),sin(θ+
)),
=(1,0)
则f(θ)=
•
+2S=cos(θ+
)+sinθ=sin(θ+
)
∵θ∈(0,π),故θ=
时,f(θ)max=1;
(2)由题意,cosθ=-
,sinθ=
,在△BOC中,∠BOC=θ+
,由余弦定理得:|
|2=1+1-2×1×1×cos(θ+
)=2-
cosθ+sinθ=
.
| 1 |
| 2 |
| OB |
| π |
| 6 |
| π |
| 6 |
| OC |
则f(θ)=
| OB |
| OC |
| π |
| 6 |
| π |
| 3 |
∵θ∈(0,π),故θ=
| π |
| 6 |
(2)由题意,cosθ=-
| 3 |
| 5 |
| 4 |
| 5 |
| π |
| 6 |
| BC |
| π |
| 6 |
| 3 |
14+3
| ||
| 5 |
点评:本题主要考查了余弦定理的运用.余弦定理是解三角形问题的常用方法,要熟练掌握余弦定理及其变式的应用.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
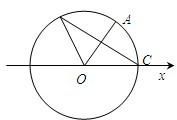 如图,A、B是单位圆O上的动点,C是圆与x轴正半轴的交点,设∠COA=α.
如图,A、B是单位圆O上的动点,C是圆与x轴正半轴的交点,设∠COA=α.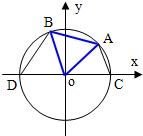 如图,A、B是单位圆O上的点,C、D分别是圆O与x轴的两个交点,△ABO为正三角形.
如图,A、B是单位圆O上的点,C、D分别是圆O与x轴的两个交点,△ABO为正三角形.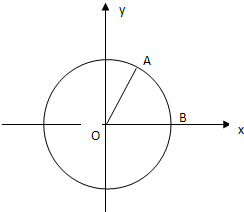 如图,A,B是单位圆上的两个质点,B点坐标为(1,0),∠BOA=60°,质点A以1弧度/秒的角速度按逆时针方向在单位圆上运动;质点B以1弧度/秒的角速度按顺时针方向在单位圆上运动,过点A作AA1⊥y轴于A1,过点B作BB1⊥y轴于B1.
如图,A,B是单位圆上的两个质点,B点坐标为(1,0),∠BOA=60°,质点A以1弧度/秒的角速度按逆时针方向在单位圆上运动;质点B以1弧度/秒的角速度按顺时针方向在单位圆上运动,过点A作AA1⊥y轴于A1,过点B作BB1⊥y轴于B1.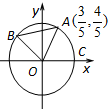 如图,A、B是单位圆O上的点,C是圆O与x轴正半轴的交点,点A的坐标为
如图,A、B是单位圆O上的点,C是圆O与x轴正半轴的交点,点A的坐标为