题目内容
已知函数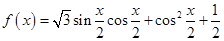 (1)求
(1)求 的单调减区间;(2)在锐角三角形ABC中,A、B、C的对边
的单调减区间;(2)在锐角三角形ABC中,A、B、C的对边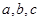 且满足
且满足 ,求
,求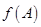 的取值范围.
的取值范围.
(1)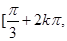
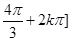
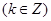 ;(2)
;(2)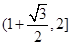
解析试题分析:(1)求函数的单调区间需将已知化为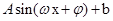 的形式,然后利用复合函数的单调性处理,先逆用正弦的二倍角公式和降幂公式,然后利用辅助角公式即可求;(2)三角形问题中,如果有边角混合的式子,可考虑边角转化,或变为关于角的三角关系式,或变为关于边的代数式处理,该题先利用正弦定理把边化角,得三角关系式,从中解
的形式,然后利用复合函数的单调性处理,先逆用正弦的二倍角公式和降幂公式,然后利用辅助角公式即可求;(2)三角形问题中,如果有边角混合的式子,可考虑边角转化,或变为关于角的三角关系式,或变为关于边的代数式处理,该题先利用正弦定理把边化角,得三角关系式,从中解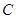 ,然后结合已知条件得
,然后结合已知条件得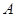 的范围(注意
的范围(注意 是锐角三角形这个条件),然后确定
是锐角三角形这个条件),然后确定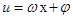 的范围,再结合
的范围,再结合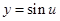 的图象求
的图象求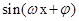 的范围,从而可求出
的范围,从而可求出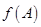 的取值范围.
的取值范围.
试题解析:(1)由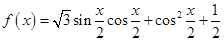 得
得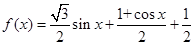 =
=
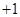 ,∴
,∴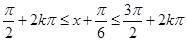 ,解得
,解得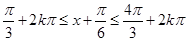 ,
,
故 的单调减区间为
的单调减区间为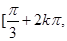
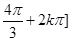
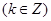 ;
;
(2)因为 ,由正弦定理得
,由正弦定理得
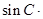
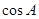 ,化简为
,化简为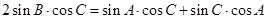 ,所以
,所以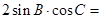
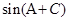 =
=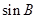 ,∴
,∴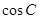 =
= ,又因为
,又因为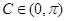 ,所以
,所以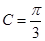 ,由
,由 是锐角三角形,所以
是锐角三角形,所以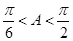 ,
, 
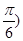
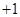 ,
,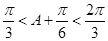 ,∴
,∴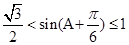 ,∴
,∴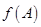 的取值范围.为
的取值范围.为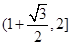 .
.
考点:1、三角函数的单调区间;2、正弦定理;3、三角函数的值域.

练习册系列答案
相关题目
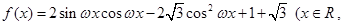
 >
> 的最小正周期是
的最小正周期是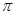 .
. <
< 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.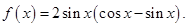
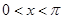 时,求
时,求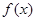 的最大值及相应的x值;
的最大值及相应的x值;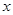 的图象经过怎样的变换得到f(x)的图象.
的图象经过怎样的变换得到f(x)的图象.  .
. 的最小正周期及最小值;
的最小正周期及最小值; 为锐角,且
为锐角,且 ,求
,求 ,
,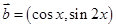 ,
, .
.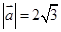 ,求
,求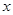 的值;
的值;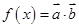 ,求
,求 的最大、最小值.
的最大、最小值.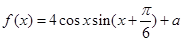 的最大值为2.
的最大值为2.
 的值及
的值及 的最小正周期;
的最小正周期;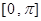 上的图像.
上的图像. 为偶函数,周期为2
为偶函数,周期为2 .
.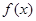 的解析式;
的解析式; 的值.
的值. .
. 的最小正周期;
的最小正周期; 中,
中,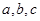 分别是
分别是 A、
A、 ,
, ,
, ,求
,求 的值.
的值. ,
, 时,求
时,求 在区间
在区间 上的取值范围;
上的取值范围;
 =2时,
=2时, =
= ,求
,求 的值。
的值。