Question

【题目】已知a＞0，函数f（x）＝|2x+2|+|x﹣a|的最小值为2．

（1）求实数a的值，并作出y＝f（x）的图象；

（2）当m＞0，n＞0，且m+n＝2时，m2+n2≥f（x）恒成立，求实数x的取值范围．

Answer 1

【答案】（1）a＝1，见解析（2）{x|}．

【解析】

（1）分段讨论求出的最小值，且等于，即可求解；

（2）由基本不等式求出的最小值为4，分段讨论解不等式，即可得出结论.

（1），

当；

当；

当，

所以的最小值为，

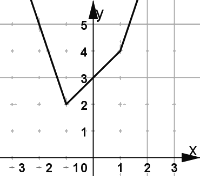
f（x）的图象如图所示：

（2）∵m＞0，n＞0且m+n＝2，

∴，当且仅当m＝n时等号成立，

∴（m2+n2）min＝4，∵m2+n2≥f（x）恒成立，

∴f（x）≤（m2+n2）min＝4，

∴|2x+2|+|x﹣1|≤4，

∴或或，

∴﹣1≤x≤1或，

∴，

∴不等式的解集为{x|}．