题目内容
10.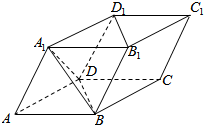 如图,四棱柱ABCD-A1B1C1D1中,所有棱长均为a,且∠A1AB=∠A1AD=∠DAB=60°,则下列结论正确的是①②④⑤(写出所有正确的结论的编号).
如图,四棱柱ABCD-A1B1C1D1中,所有棱长均为a,且∠A1AB=∠A1AD=∠DAB=60°,则下列结论正确的是①②④⑤(写出所有正确的结论的编号).①平面A1BD∥平面CB1D1;
②四边形BDD1B1为正方形;
③点A到平面BDD1B1的距离为$\frac{\sqrt{3}}{2}$a;
④点A1在平面BDC1上的射影为△BDC1的垂心;
⑤平面A1BD与平面BDD1B1将四棱柱分成从小到大三部分的体积比为1:2:3.
分析 由A1D∥B1C,A1B∥D1C,推导出①正确;由A1-ABD是正四面体推导出②正确;由A1-BDD1B1是正四棱锥,推导出③错误;由三棱锥C1-A1BD为正三棱锥,推导出④正确;由A1-ABD占总体的$\frac{1}{6}$,BDC-B1D1C1占总体的$\frac{1}{2}$,A1-BDD1B1占总体的$\frac{1}{3}$,推导出⑤正确.
解答 解:对于①:由图得A1D∥B1C,A1B∥D1C,
∴平面A1BD∥平面CB1D1,故①正确;
对于②:∵A1-ABD是正四面体,∴AA1⊥BD,
∴DD1⊥BD,∴四边形BDD1B1为正方形,故②正确;
对于③:A1-BDD1B1是正四棱锥,所有棱长均相等,
A到平面BDD1B1的距离等于A1到平面BDD1B1的距离,
等于A1到BDD1B1的距离,为$\frac{\sqrt{2}}{2}a$,故③错误;
对于④:三棱锥C1-A1BD为正三棱锥,对棱互相垂直,
则A1在平面BDC1上的射影为△BDC1的垂心,故④正确;
对于⑤:A1-ABD占总体的$\frac{1}{6}$,BDC-B1D1C1占总体的$\frac{1}{2}$,A1-BDD1B1占总体的$\frac{1}{3}$,
∴平面A1BD与平面BDD1B1将四棱柱分成从小到大三部分的体积比为1:2:3,故⑤正确.
故答案为:①②④⑤.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意棱柱的结构特征和空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
相关题目
15.双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1与直线y=x+b相切,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{3}$ |
19.某人制定了一项旅游计划,从7个旅游城市中选5个进行游览,如果A、B、C为必选城市,并且游览过程中必须按照先A后B再C的次序经过A、B、C三个城市(A、B、C三个城市可以不相邻),则不同的游览线路共有( )
| A. | 80种 | B. | 120种 | C. | 480种 | D. | 600种 |
20.等差数列{an}的前n项之和为Sn,若a2+a6+a10=18,则a6是( )
| A. | 15 | B. | 15 | C. | 20 | D. | 6 |
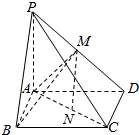 已知在四棱锥P-ABCD中,平面ABCD是平行四边形,侧棱PA⊥平面ABCD,M、N分别为PD、AC的中点.
已知在四棱锥P-ABCD中,平面ABCD是平行四边形,侧棱PA⊥平面ABCD,M、N分别为PD、AC的中点.