题目内容
18.甲乙两个人参加射击训练,射击一次中靶的概率分别是p1,p2,其中$\frac{1}{{p}_{1}}$,$\frac{1}{{p}_{2}}$是函数f(x)=$\frac{1}{3}$x3-$\frac{5}{2}$x2+6x的两极值点(p1>p2).(1)求p1,p2的值;
(2)两人各射击1次,求两人中恰好有一人中靶的概率.
分析 (1)求导数,f′(x)=(x-2)(x-3),导数为0的实数根为2,3,从而2,3便为f(x)的两极值点,根据p1>p2,便可得出${p}_{1}=\frac{1}{2},{p}_{2}=\frac{1}{3}$;
(2)事件“两人中恰有一人中靶”,包含“甲中靶乙不中靶”和“乙中靶甲不中靶”两个事件,这两个事件显然互斥,从而分别求出这两个事件的概率再求和即可.
解答 解:(1)f′(x)=x2-5x+6=(x-2)(x-3);
∴2,3是f(x)的两个极值点;
p1>p2;
∴$\frac{1}{{p}_{1}}<\frac{1}{{p}_{2}}$;
∴$\frac{1}{{p}_{1}}=2,\frac{1}{{p}_{2}}=3$;
∴${p}_{1}=\frac{1}{2},{p}_{2}=\frac{1}{3}$;
(2)甲中靶乙未中靶的概率为$\frac{1}{2}×(1-\frac{1}{3})=\frac{1}{3}$;
乙中靶甲未中靶的概率为$(1-\frac{1}{2})×\frac{1}{3}=\frac{1}{6}$;
∴两人中恰有一人中靶的概率为$\frac{1}{3}+\frac{1}{6}=\frac{1}{2}$.
点评 考查函数极值点的概念,及极值点的求法,函数在极值点处导数的取值情况,以及独立重复试验的概念,及互斥事件的概率的求法.

练习册系列答案
相关题目
6.等比数列{an}中,a2=2,a5=$\frac{1}{4}$,则公比q=( )
| A. | -$\frac{1}{2}$ | B. | -2 | C. | 2 | D. | $\frac{1}{2}$ |
 如图,在斜三棱柱ABC-A1B1C1中,D是BC的中点,求证:A1C∥平面AB1D.
如图,在斜三棱柱ABC-A1B1C1中,D是BC的中点,求证:A1C∥平面AB1D.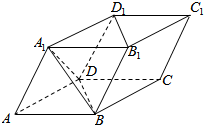 如图,四棱柱ABCD-A1B1C1D1中,所有棱长均为a,且∠A1AB=∠A1AD=∠DAB=60°,则下列结论正确的是①②④⑤(写出所有正确的结论的编号).
如图,四棱柱ABCD-A1B1C1D1中,所有棱长均为a,且∠A1AB=∠A1AD=∠DAB=60°,则下列结论正确的是①②④⑤(写出所有正确的结论的编号).