题目内容
已知函数![]() ,其中
,其中![]() 是
是![]() 的导函数。
的导函数。
(1)若![]() 在
在![]() 处的导数为4,求实数
处的导数为4,求实数![]() 的值;
的值;
(2)对满足![]() 的一切
的一切![]() 的值,都有
的值,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,函数
时,函数![]() 的图象与直线
的图象与直线![]() 只有一个公共点,
只有一个公共点,
求实数![]() 的取值范围。
的取值范围。
解:(1) ![]() ,
,![]()
![]() ,
,![]() ; …………(2分)
; …………(2分)
(2) ![]() ,令
,令![]() ,
,
![]() 对满足
对满足![]() 的一切
的一切![]() 的值,都有
的值,都有![]() ,即 对于
,即 对于![]() 都有
都有![]() ;
;
上述条件等价于在![]() 上
上![]() ; ………(4分)
; ………(4分)
明显的,当![]() 时,不满足条件;
时,不满足条件;
当![]() 时,
时, ![]() 在
在![]() 上上单调递增,
上上单调递增,
则![]() ,解得:
,解得:![]() ,
,
所以 ![]() ;
;
当![]() 时,
时, ![]() 在
在![]() 上上单调递减,
上上单调递减,
则![]() ,解得:
,解得: ![]() ,
,
所以![]() 不存在;
不存在;
综上所得,实数![]() 的取值范围是
的取值范围是![]() ; ……(8分)
; ……(8分)
(3)![]() ,
, ![]() ,
,![]() ,
,
令![]() ,解得:
,解得:![]() ,
,
令![]() ,解得:
,解得: ![]() ;
;
![]() 在
在![]() 上单调增,在
上单调增,在![]() 上单调减, ……(10分)
上单调减, ……(10分)
要使得函数![]() 的图象与直线
的图象与直线![]() 只有一个公共点,
只有一个公共点,
只要满足:![]() ,即
,即![]() ……(13分)
……(13分)
![]() ……(14分)
……(14分)

练习册系列答案
相关题目
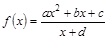 (其中
(其中 是实数常数,
是实数常数, )
) ,函数
,函数 的图像关于点(—1,3)成中心对称,求
的图像关于点(—1,3)成中心对称,求 的值;
的值; ,总有
,总有 ,求
,求 的取值范围;
的取值范围; ,
, ,且对任意
,且对任意 时,不等式
时,不等式 恒成立,求负实数
恒成立,求负实数 的取值范围.
的取值范围.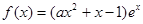 ,其中
,其中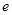 是自然对数的底数,
是自然对数的底数,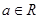 .
.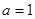 ,求曲线
,求曲线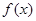 在点
在点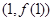 处的切线方程;
处的切线方程; ,求
,求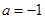 ,函数
,函数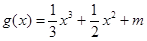 的图象有3个不同的交点,求实数
的图象有3个不同的交点,求实数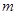 的取值范围.
的取值范围. 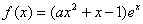 ,其中
,其中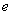 是自然对数的底数,
是自然对数的底数,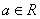 .
.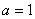 ,求曲线
,求曲线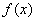 在点
在点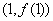 处的切线方程;
处的切线方程;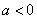 ,求
,求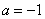 ,函数
,函数 的图象有3个不同的交点,求实数
的图象有3个不同的交点,求实数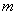 的取值范围.
的取值范围.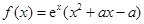 ,其中
,其中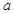 是常数.
是常数. (1)当
(1)当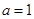 时,求曲线
时,求曲线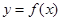 在点
在点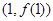 处的切线方程;
处的切线方程; ,使得关于
,使得关于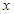 的方程
的方程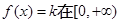 上有两个不相等的实数根,求
上有两个不相等的实数根,求