题目内容
8.设A,B是抛物线C:y2=2px(p>0)上的两个动点,线段AB的中点为M,F为抛物线C的焦点,且∠AFB=60°,过M作抛物线C的准线l的垂线,垂足为N,则$\frac{{|{AB}|}}{{|{MN}|}}$的取值范围为[1,2).分析 先设出|AF|,|BF|分别过A,B,M作准线的垂线,垂足分别是A′,B′,N,进而表示出|MN|,利用余弦定理表示出|AB|利用基本不等式求得其范围,最后求得$\frac{{|{AB}|}}{{|{MN}|}}$的最小值,利用两边之和大于第三边,即可得出结论.
解答 解:设|AF|=r1,|BF|=r2,分别过A,B,M作准线的垂线,垂足分别是A′,B′,N,则|MN|=$\frac{{r}_{1}+{r}_{2}}{2}$,
由余弦定理得|AB|2=r12+r22-2r1r2cos60°=(r1+r2)2-3r1r2≥$\frac{1}{4}$(r1+r2)2,
∴($\frac{{|{AB}|}}{{|{MN}|}}$)2≥1,
∴$\frac{{|{AB}|}}{{|{MN}|}}$的最小值为1.
∵|AF|+|BF|>|AB|,∴2|MN|>|AB|,
∴$\frac{{|{AB}|}}{{|{MN}|}}$<2
故答案为:[1,2).
点评 本题主要考查了抛物线的简单性质.注重了学生对基础知识综合运用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
16.设f(x)=2(log2x)2+2alog2$\frac{1}{x}$+b,已知x=$\frac{1}{2}$时,f(x)有最小值-8,
(1)求a与b的值;
(2)求满足f(x)>0的x的集合A.
(1)求a与b的值;
(2)求满足f(x)>0的x的集合A.
20.若函数f(x)=x2+ax+$\frac{1}{x}$在($\frac{1}{2}$,+∞)上是增函数,则a的取值范围是( )
| A. | [-1,0] | B. | [-1,+∞) | C. | [0,3] | D. | [3,+∞) |
8.从0,1,2,3,4,5,6七个数中任取两个数相乘,使所得的积为偶数,这样的偶数共有( )个.
| A. | 18 | B. | 9 | C. | 12 | D. | 11 |
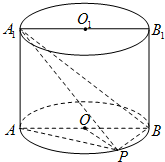 如图,ABB1A1为圆柱的轴截面,点P为圆柱下底面圆周上异于A,B的一点.求证:BP⊥A1P.
如图,ABB1A1为圆柱的轴截面,点P为圆柱下底面圆周上异于A,B的一点.求证:BP⊥A1P.