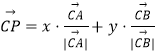Question

【题目】已知函数是定义在上的奇函数，且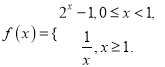偶函数的定义域为，且当时， .若存在实数，使得成立，则实数的取值范围是（ ）

A. B. C. D.

Answer 1

【答案】D

【解析】∵，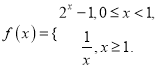

∴当0≤x≤1时，2x﹣1∈[0，1]，

当x≥1时， ∈（0，1]，

即x≥0时，f（x）的值域为[0，1]，

∵f（x）是定义在R上的奇函数，∴x≤0时f（x）的值域为[﹣1，0]，

∴在R上的函数f（x）的值域为[﹣1，1]．

∵定义在{x|x≠0}上的偶函数g（x），x＞0的g（x）=log2x，

∴g（x）=log2|x|（x≠0）

∵存在实数a，使得f（a）=g（b）成立，

∴令﹣1≤g（b）≤1．

即﹣1≤log2|b|≤1．

即有≤|b|≤2，

∴≤b≤2或﹣2≤b≤﹣．

故选：D．