题目内容
(2013•石景山区一模)设抛物线y2=4x的焦点为F,其准线与x轴的交点为Q,过点F作直线l交抛物线于A、B两点,若∠AQB=90°,则直线l的方程为
x=1
x=1
.分析:设A(x1,y1),B(x2,y2),由∠AQB=90°得kAQ•kBQ=-1,建立关系式并化简得-y1y2=x1x2+(x1+x2)+1,再根据抛物线的性质将x1x2=1和y1y2=-4代入计算,可得x1=x2=1,即可得到直线l的方程.
解答:解: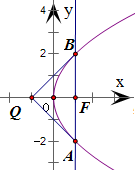 设A(x1,y1),B(x2,y2)
设A(x1,y1),B(x2,y2)
∵∠AQB=90°,
∴kAQ•kBQ=-1,可得
•
=-1,即-y1y2=(x1+1)(x2+1)
整理可得-y1y2=x1x2+(x1+x2)+1…(*)
∵直线AB经过抛物线y2=4x的焦点F(1,0)
∴根据抛物线的性质,可得x1x2=
p2=1,y1y2=-p2=-4
代入(*)得:4=1+(x1+x2)+1,可得x1+x2=2
结合x1x2=1,可得x1=x2=1,即A、B两点的横坐标相等,
∴直线AB的方程为x=1,即直线l的方程为x=1
故答案为:x=1
 设A(x1,y1),B(x2,y2)
设A(x1,y1),B(x2,y2)∵∠AQB=90°,
∴kAQ•kBQ=-1,可得
| y1 |
| x1+1 |
| y2 |
| x2+1 |
整理可得-y1y2=x1x2+(x1+x2)+1…(*)
∵直线AB经过抛物线y2=4x的焦点F(1,0)
∴根据抛物线的性质,可得x1x2=
| 1 |
| 4 |
代入(*)得:4=1+(x1+x2)+1,可得x1+x2=2
结合x1x2=1,可得x1=x2=1,即A、B两点的横坐标相等,
∴直线AB的方程为x=1,即直线l的方程为x=1
故答案为:x=1
点评:本题给出抛物线的焦点弦AB的端点对点Q(-1,0)的张角等于90度,求直线AB的方程,着重考查了抛物线的定义与简单几何性质等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•石景山区一模)某四棱锥的三视图如图所示,则最长的一条侧棱长度是( )
(2013•石景山区一模)某四棱锥的三视图如图所示,则最长的一条侧棱长度是( )