题目内容
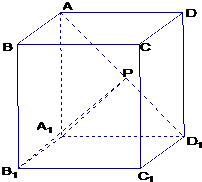 如图,已知ABCD-A1B1C1D1是底面为正方形的长方体,∠AD1A1=60°,AD1=4,点P是AD1上的动点.
如图,已知ABCD-A1B1C1D1是底面为正方形的长方体,∠AD1A1=60°,AD1=4,点P是AD1上的动点.(1)试求四棱锥P-A1B1C1D1体积的最大值;
(2)试判断不论点P在AD1上的任何位置,是否都有平面B1PA1垂直于平面AA1D1?并证明你的结论.
分析:(1)由棱锥的体积公式,由底面A1B1C1D1的面积固定,则四棱锥P-A1B1C1D1的高取最大值时,四棱锥P-A1B1C1D1体积取最大值,结合P是AD1上的动点,易得当P与A重合时满足条件,代入棱锥的体积公式,即可求出答案.
(2)由题意知,B1A1⊥A1D1,B1A1⊥A1A,由线面垂直的判定定理,可得B1A1⊥平面AA1D1,进而由面面垂直判定得到平面B1PA1垂直于平面AA1D1.
(2)由题意知,B1A1⊥A1D1,B1A1⊥A1A,由线面垂直的判定定理,可得B1A1⊥平面AA1D1,进而由面面垂直判定得到平面B1PA1垂直于平面AA1D1.
解答:解:(1)∵ABCD-A1B1C1D1是长方体∴侧面AA1D1⊥底面A1B1C1D1
∴四棱锥P-A1B1C1D1的高为点P到平面A1B1C1D1的距离
当点P与点A重合时,四棱锥P-A1B1C1D1的高取得最大值,这时四棱锥P-A1B1C1D1体积最大,
在 Rt△AA1D1中∵∠AD1A1=60°
∴AA1=AD1sin60°=2
,A1D1=AD1cos60°=2,
∴(VP-A1B1C1D1)max=
•SA1B1C1D1•AA1=
(2)不论点P在AD1上的任何位置,都有平面B1PA1垂直于平面AA1D1.证明如下:
由题意知,B1A1⊥A1D1,B1A1⊥A1A,
又∵AA1∩A1D1=A1
∴B1A1⊥平面AA1D1
又A1B1?平面B1PA1
∴平面B1PA1⊥平面AA1D1.
∴四棱锥P-A1B1C1D1的高为点P到平面A1B1C1D1的距离
当点P与点A重合时,四棱锥P-A1B1C1D1的高取得最大值,这时四棱锥P-A1B1C1D1体积最大,
在 Rt△AA1D1中∵∠AD1A1=60°
∴AA1=AD1sin60°=2
| 3 |
∴(VP-A1B1C1D1)max=
| 1 |
| 3 |
| 8 |
| 3 |
| 3 |
(2)不论点P在AD1上的任何位置,都有平面B1PA1垂直于平面AA1D1.证明如下:
由题意知,B1A1⊥A1D1,B1A1⊥A1A,
又∵AA1∩A1D1=A1
∴B1A1⊥平面AA1D1
又A1B1?平面B1PA1
∴平面B1PA1⊥平面AA1D1.
点评:本题考查的知识点是平面与平面垂直的判定,棱锥的体积公式,其中(1)的关键是判断出当P与A重合时满足四棱锥P-A1B1C1D1体积取最大值,(2)的关键是证得B1A1⊥平面AA1D1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 18、如图,已知ABCD是矩形,E是以CD为直径的半圆周上一点,且平面CDE⊥平面ABCD,求证:CE⊥平面ADE.
18、如图,已知ABCD是矩形,E是以CD为直径的半圆周上一点,且平面CDE⊥平面ABCD,求证:CE⊥平面ADE.
 (2012•汕头二模)如图,已知ABCD-A1B1C1D1是底面边长为1的正四棱柱,
(2012•汕头二模)如图,已知ABCD-A1B1C1D1是底面边长为1的正四棱柱, 如图,已知ABCD是正方形,DE⊥平面ABCD,BF⊥平面ABCD,且AB=FB=2DE.
如图,已知ABCD是正方形,DE⊥平面ABCD,BF⊥平面ABCD,且AB=FB=2DE. (2005•普陀区一模)如图,已知ABCD和A1B1C1D1都是正方形,且AB∥A1B1,AA1=BB1=CC1=DD1,若将图中已作出的线段的两个端点分别作为向量的始点和终点所形成的不相等的向量的全体构成集合M,则从集合M中任取两个向量恰为平行向量的概率是
(2005•普陀区一模)如图,已知ABCD和A1B1C1D1都是正方形,且AB∥A1B1,AA1=BB1=CC1=DD1,若将图中已作出的线段的两个端点分别作为向量的始点和终点所形成的不相等的向量的全体构成集合M,则从集合M中任取两个向量恰为平行向量的概率是