题目内容
已知函数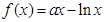 ,
,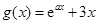 ,其中
,其中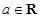 .
.
(Ⅰ)求 的极值;
的极值;
(Ⅱ)若存在区间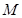 ,使
,使 和
和 在区间
在区间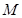 上具有相同的单调性,求
上具有相同的单调性,求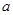 的取值范围.
的取值范围.
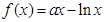 ,
,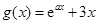 ,其中
,其中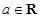 .
.(Ⅰ)求
 的极值;
的极值;(Ⅱ)若存在区间
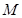 ,使
,使 和
和 在区间
在区间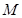 上具有相同的单调性,求
上具有相同的单调性,求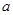 的取值范围.
的取值范围.(Ⅰ)极小值为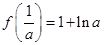 ;没有极大值(Ⅱ)
;没有极大值(Ⅱ)
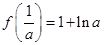 ;没有极大值(Ⅱ)
;没有极大值(Ⅱ)
(Ⅰ)解: 的定义域为
的定义域为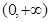 ,………………1分
,………………1分
且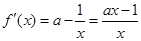 . ………………2分
. ………………2分
① 当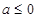 时,
时,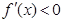 ,故
,故 在
在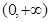 上单调递减.
上单调递减.
从而 没有极大值,也没有极小值. ………………3分
没有极大值,也没有极小值. ………………3分
② 当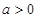 时,令
时,令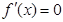 ,得
,得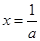 .
.
 和
和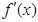 的情况如下:
的情况如下:
故 的单调减区间为
的单调减区间为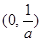 ;单调增区间为
;单调增区间为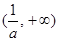 .
.
从而 的极小值为
的极小值为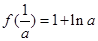 ;没有极大值.………………5分
;没有极大值.………………5分
(Ⅱ)解: 的定义域为
的定义域为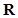 ,且
,且 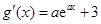 .………………6分
.………………6分
③ 当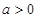 时,显然
时,显然  ,从而
,从而 在
在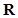 上单调递增.
上单调递增.
由(Ⅰ)得,此时 在
在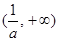 上单调递增,符合题意. ………………8分
上单调递增,符合题意. ………………8分
④ 当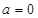 时,
时, 在
在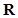 上单调递增,
上单调递增, 在
在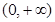 上单调递减,不合题意.……9分
上单调递减,不合题意.……9分
⑤ 当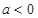 时,令
时,令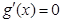 ,得
,得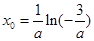 .
. 和
和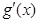 的情况如下表:
的情况如下表:
当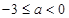 时,
时,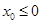 ,此时
,此时 在
在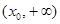 上单调递增,由于
上单调递增,由于 在
在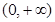 上单调递减,不合题意. ………………11分
上单调递减,不合题意. ………………11分
当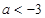 时,
时,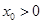 ,此时
,此时 在
在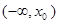 上单调递减,由于
上单调递减,由于 在
在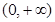 上单调递减,符合题意.
上单调递减,符合题意.
综上,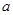 的取值范围是
的取值范围是 . ………………13
. ………………13
 的定义域为
的定义域为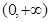 ,………………1分
,………………1分且
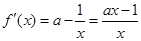 . ………………2分
. ………………2分① 当
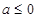 时,
时,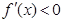 ,故
,故 在
在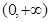 上单调递减.
上单调递减.从而
 没有极大值,也没有极小值. ………………3分
没有极大值,也没有极小值. ………………3分② 当
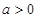 时,令
时,令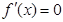 ,得
,得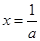 .
.  和
和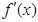 的情况如下:
的情况如下: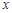 | 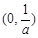 | 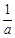 | 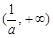 |
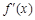 | 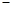 | 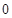 | 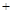 |
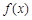 | ↘ | | ↗ |
 的单调减区间为
的单调减区间为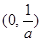 ;单调增区间为
;单调增区间为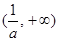 .
.从而
 的极小值为
的极小值为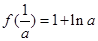 ;没有极大值.………………5分
;没有极大值.………………5分(Ⅱ)解:
 的定义域为
的定义域为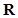 ,且
,且 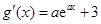 .………………6分
.………………6分③ 当
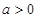 时,显然
时,显然  ,从而
,从而 在
在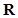 上单调递增.
上单调递增.由(Ⅰ)得,此时
 在
在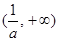 上单调递增,符合题意. ………………8分
上单调递增,符合题意. ………………8分④ 当
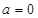 时,
时, 在
在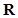 上单调递增,
上单调递增, 在
在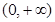 上单调递减,不合题意.……9分
上单调递减,不合题意.……9分⑤ 当
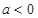 时,令
时,令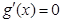 ,得
,得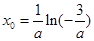 .
. 和
和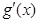 的情况如下表:
的情况如下表: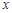 | 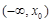 | 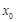 | 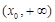 |
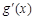 | 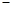 | 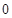 | 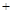 |
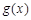 | ↘ | | ↗ |
当
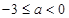 时,
时,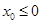 ,此时
,此时 在
在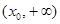 上单调递增,由于
上单调递增,由于 在
在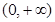 上单调递减,不合题意. ………………11分
上单调递减,不合题意. ………………11分当
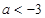 时,
时,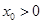 ,此时
,此时 在
在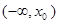 上单调递减,由于
上单调递减,由于 在
在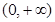 上单调递减,符合题意.
上单调递减,符合题意. 综上,
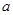 的取值范围是
的取值范围是 . ………………13
. ………………13
练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目

 ,求
,求 的极大值点;
的极大值点; 且
且 的取值范围.
的取值范围. .
. 时,求
时,求 的最大值;
的最大值; 恒成立;
恒成立; .(参考数据:
.(参考数据: )
)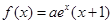 (其中
(其中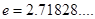 ),
),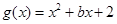 ,已知它们在
,已知它们在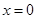 处有相同的切线.
处有相同的切线.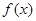 ,
,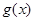 的解析式;
的解析式; 上的最小值;
上的最小值;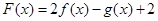 零点个数.
零点个数.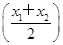 >0.
>0. 的导函数为f¢(x),则f¢(1)的值为 .
的导函数为f¢(x),则f¢(1)的值为 .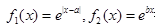
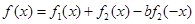 ,是否存在a,b
,是否存在a,b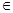 R,y=f(x)为偶函数.如果存在.请举例并证明你的结论,如果不存在,请说明理由;
R,y=f(x)为偶函数.如果存在.请举例并证明你的结论,如果不存在,请说明理由;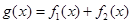 在R上的单调区间;
在R上的单调区间;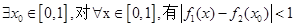 成立.求a的取值范围.
成立.求a的取值范围. x3+
x3+ x2+tan θ,其中θ∈
x2+tan θ,其中θ∈ ,则导数f′(1)的取值范围是( )
,则导数f′(1)的取值范围是( ) ,
, ]
]