题目内容
【题目】在平面直角坐标系xoy中,圆O的参数方程为![]() (
(![]() 为参数).过点(
为参数).过点(![]() )且倾斜角为
)且倾斜角为![]() 的直线
的直线![]() 与圆O交于A、B两点.
与圆O交于A、B两点.
(1)求![]() 的取值范围;
的取值范围;
(2)求AB中点P的轨迹的参数方程.
【答案】(1)![]() (2)
(2)
【解析】
(1)⊙O的普通方程为x2+y2=1,圆心为O(0,0),半径r=1,当α=![]() 时,直线l的方程为x=0,成立;当α≠
时,直线l的方程为x=0,成立;当α≠![]() 时,过点(0,﹣
时,过点(0,﹣![]() )且倾斜角为α的直线l的方程为y=tanαx+
)且倾斜角为α的直线l的方程为y=tanαx+![]() ,从而圆心O(0,0)到直线l的距离d=
,从而圆心O(0,0)到直线l的距离d=![]() <1,进而求出
<1,进而求出![]() 或
或![]() ,由此能求出α的取值范围.
,由此能求出α的取值范围.
(2)设直线l的方程为x=m(y+![]() ),联立
),联立![]() ,得(m2+1)y2+2
,得(m2+1)y2+2![]() +2m2﹣1=0,由此利用韦达定理、中点坐标公式能求出AB中点P的轨迹的参数方程.
+2m2﹣1=0,由此利用韦达定理、中点坐标公式能求出AB中点P的轨迹的参数方程.
(1)圆O的直角坐标方程为:![]() ,当
,当![]() 时,
时,![]() 与圆O交于两点,
与圆O交于两点,
当![]() 时,设
时,设![]() ,则
,则![]() 的方程为:
的方程为:![]()
![]() 与圆O交于两点当且仅当
与圆O交于两点当且仅当![]()
解得:![]() 或
或![]() ,即
,即![]() 或
或![]() ,
,
![]() .
.
(2) ![]() 的参数方程为:
的参数方程为:![]()
![]() ,
,
![]() ,
,
![]()
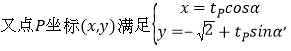 ,
,
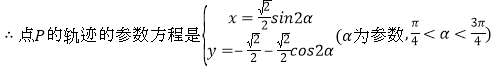 .
.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
【题目】一台机器由于使用时间较长,生产的零件有一些缺损.按不同转速生产出来的零件有缺损的统计数据如下表所示:
转速x(转/秒) | 16 | 4 | 12 | 8 |
每小时生产有缺损零件数y(个) | 11 | 9 | 8 | 5 |
(1)作出散点图;
(2)如果y与x线性相关,求出回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么,机器的运转速度应控制在什么范围内?

