题目内容
设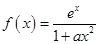 ,其中
,其中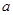 为正实数.
为正实数.
(1)当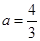 时,求
时,求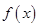 的极值点;
的极值点;
(2)若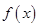 为
为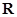 上的单调函数,求
上的单调函数,求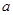 的取值范围.
的取值范围.
【答案】
(1)x1= 是极小值点,x2=
是极小值点,x2=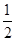 是极大值点.
是极大值点.
(2)a的取值范围为(0,1].
【解析】
试题分析:解 对f(x)求导得
f′(x)=ex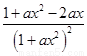 . ①
. ①
(1)当a=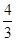 时,令f′(x)=0,则4x2-8x+3=0,解得x1=
时,令f′(x)=0,则4x2-8x+3=0,解得x1= ,x2=
,x2=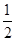 .
.
结合①,可知
|
x |
|
|
|
|
|
|
f′(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
? |
极大值 |
? |
极小值 |
? |
所以,x1= 是极小值点,x2=
是极小值点,x2=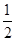 是极大值点.
是极大值点.
(2)若f(x)为R上的单调函数,则f′(x)在R上不变号,
结合①与条件a>0,知ax2-2ax+1≥0在R上恒成立,
因此Δ=4a2-4a=4a(a-1)≤0,由此并结合a>0,知0<a≤1.所以a的取值范围为(0,1].
考点:导数的运用
点评:解决的关键是根据导数的符号判定函数单调性,以及函数极值的运用,属于中档题。

练习册系列答案
相关题目


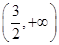
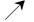

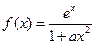 ,其中
,其中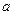 为正实数
为正实数 时,求
时,求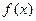 的极值点;
的极值点;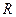 上的单调函数,求
上的单调函数,求 围。
围。 ,其中
,其中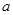 为正实数。
为正实数。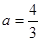 时,求
时,求 的极值点;
的极值点;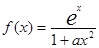 ,其中
,其中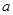 为正实数.
为正实数.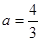 时,求
时,求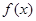 的极值点;
的极值点;
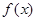 为R上的单调函数,求
为R上的单调函数,求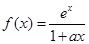 ,其中
,其中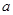 为正实数
为正实数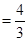 时,求
时,求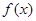 的极值点;
的极值点;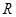 上的单调函数,求
上的单调函数,求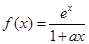 ,其中
,其中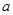 为正实数
为正实数 时,求
时,求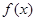 的极值点;
的极值点;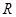 上的单调函数,求
上的单调函数,求