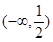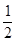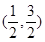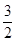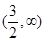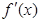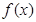题目内容
．（本小题满分12分）
设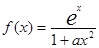
，其中
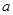为正实数.
（Ⅰ）当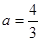
时，求
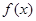的极值点；
（Ⅱ）若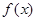
为R上的单调函数，求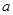的取值范围.
【答案】
（Ⅰ）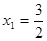
是极小值点,
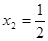是极大值点.（II）a的取值范围是0＜a≤1。
【解析】本试题考查了导数在研究函数中的运用。
（1）根据已知函数求解定义域和导数，然后分析单调性，从而得到极值。
（2）因为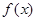
为R上的单调函数，则说明了
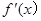在R上不变号，由
知，
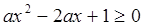在R上恒成立，
可知判别式小于等于零即可。
解：对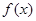
求导得 ①
（Ⅰ）当
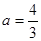，若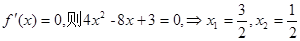
|
x |
|
|
|
|
|
|
|
+ |
0 |
－ |
0 |
+ |
|
|
↗ |
极大值 |
↘ |
极小值 |
↗ |
所以,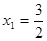是极小值点,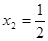是极大值点.
（II）若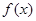为R上的单调函数，则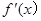在R上不变号，由知，
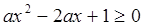在R上恒成立，
∴
故
故a的取值范围是0＜a≤1
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
