题目内容
一块边长为10cm的正方形铁片按图(1)中所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个如图(2)所示的正四棱锥形容器.在图(1)中,x表示等腰三角形的底边长;在图(2)中,点E、F分别是四棱锥P-ABCD的棱BC,PA的中点,
(1)证明:EF∥平面PDC;
(2)把该容器的体积V表示为x的函数,并求x=8cm时,三棱锥A一BEF的体积.

(1)证明:EF∥平面PDC;
(2)把该容器的体积V表示为x的函数,并求x=8cm时,三棱锥A一BEF的体积.
分析:(1)取PD的中点M,利用三角形的中位线定理、平行四边形的判定和性质及线面平行的判定定理即可证明.
(2)先找出此正四棱锥的高,进而即可求出其体积;再利用等积变形求三棱锥F-ABE即可.
(2)先找出此正四棱锥的高,进而即可求出其体积;再利用等积变形求三棱锥F-ABE即可.
解答:解:(1)证明:取PD的中点M,连接FM、CM,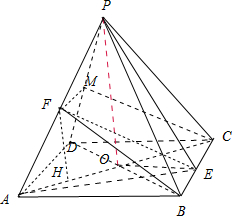
∵F为PA的中点,∴FM∥=12AD,
∵E为BC的中点,∴EC∥=12AD.
∴FM∥=EC,
∴四边形FMCE是平行四边形,∴EF∥CM.
∵EF?平面PDC,CM?平面PDC,
∴EF∥平面PDC.
(2)连接对角线AC、BD交于点O,连接OE、PO、PE.
则PO⊥底面ABCD,OE=
x,PE=5.
∴PO=
=
,
∴V四棱锥P-ABCD=
x2×
=
(0<x<10).
取AO的中点H,连接FH,则FH∥PO,FH=
PO=
.
∵PO⊥底面ABCD,∴FH⊥底面ABCD.
∴V三棱锥A-BEF=V三棱锥F-ABE=
×
×
×
x×x=
×x2,
当x=8时,V三棱锥A-BEF=
=8.

∵F为PA的中点,∴FM∥=12AD,
∵E为BC的中点,∴EC∥=12AD.
∴FM∥=EC,
∴四边形FMCE是平行四边形,∴EF∥CM.
∵EF?平面PDC,CM?平面PDC,
∴EF∥平面PDC.
(2)连接对角线AC、BD交于点O,连接OE、PO、PE.
则PO⊥底面ABCD,OE=
| 1 |
| 2 |
∴PO=
52-(
|
| ||
| 2 |
∴V四棱锥P-ABCD=
| 1 |
| 3 |
| ||
| 2 |
x2
| ||
| 6 |
取AO的中点H,连接FH,则FH∥PO,FH=
| 1 |
| 2 |
| ||
| 4 |
∵PO⊥底面ABCD,∴FH⊥底面ABCD.
∴V三棱锥A-BEF=V三棱锥F-ABE=
| 1 |
| 3 |
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 48 |
当x=8时,V三棱锥A-BEF=
| ||
| 48 |
点评:熟练掌握线面平行、垂直的判定定理和性质定理及三角形的中位线定理、平行四边形的判定及性质、锥体的体积计算公式是解题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
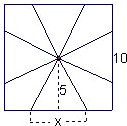 一块边长为10cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积V与x的函数关系式,并求出函数的定义域.
一块边长为10cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积V与x的函数关系式,并求出函数的定义域. (2012•南京二模)一块边长为10cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形作侧面,以它们的公共顶点p为顶点,加工成一个如图所示的正四棱锥形容器.当x=6cm时,该容器的容积为
(2012•南京二模)一块边长为10cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形作侧面,以它们的公共顶点p为顶点,加工成一个如图所示的正四棱锥形容器.当x=6cm时,该容器的容积为
 一块边长为10cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积V与x的函数关系式,并求出函数的定义域.
一块边长为10cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积V与x的函数关系式,并求出函数的定义域.