题目内容
一块边长为10cm的正方形铁片按如图1所示的虚线裁下剪开,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器.

(1)试建立容器的容积V与x的函数关系式,并求出函数的定义域.
(2)记四棱锥(如图2)的侧面积为S′,定义
为四棱锥形容器的容率比,容率比越大,用料越合理.
如果对任意的a,b∈R+,恒有如下结论:ab≤
,当且仅当a=b时取等号.试用上述结论求容率比的最大值,并求容率比最大时,该四棱锥的表面积.

(1)试建立容器的容积V与x的函数关系式,并求出函数的定义域.
(2)记四棱锥(如图2)的侧面积为S′,定义
| V |
| S′ |
如果对任意的a,b∈R+,恒有如下结论:ab≤
| a2+b2 |
| 2 |
分析:(1)设出所截等腰三角形的底边边长为xcm,在直角三角形中根据两条边长利用勾股定理做出四棱锥的高,表示出四棱锥的体积,根据实际意义写出定义域.
(2)根据所给结论计算容率比的最大值,并求出四棱锥的表面积.
(2)根据所给结论计算容率比的最大值,并求出四棱锥的表面积.
解答:解:(1)在正四棱锥E-ABCD中,底面ABCD是边长为x的正方形,
F是BC的中点,EF⊥BC,EF=5,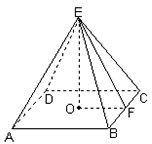
则四棱锥的高EO=
=
=
,其中0<x<10,
∴四棱锥的体积V=
×
x2
=
x2
,定义域为(0,10).
(2)侧面积S'=4×
x×5=10,
∴容率比为
=
x
≤
•
=
,
当且进行x=
,即x=5
时,
有最大值
,
此时,四棱锥的表面积S=(5
)2+4×
×5
×5=50+50
.
F是BC的中点,EF⊥BC,EF=5,

则四棱锥的高EO=
| EF2-OF2 |
25-(
|
| ||
| 2 |
∴四棱锥的体积V=
| 1 |
| 3 |
| 1 |
| 2 |
| 100-x2 |
| 1 |
| 6 |
| 100-x2 |
(2)侧面积S'=4×
| 1 |
| 2 |
∴容率比为
| V |
| S′ |
| 1 |
| 60 |
| 100-x2 |
| 1 |
| 60 |
| x2+100-x2 |
| 2 |
| 5 |
| 6 |
当且进行x=
| 00-x2 |
| 2 |
| V |
| S′ |
| 5 |
| 6 |
此时,四棱锥的表面积S=(5
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
点评:本题主要考查函数模型的应用,利用条件求出锥体的底面积和高,进而求出锥体的体积是解决本题的关键,考查学生的运算和推理能力.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
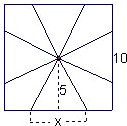 一块边长为10cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积V与x的函数关系式,并求出函数的定义域.
一块边长为10cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积V与x的函数关系式,并求出函数的定义域.
 (2012•南京二模)一块边长为10cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形作侧面,以它们的公共顶点p为顶点,加工成一个如图所示的正四棱锥形容器.当x=6cm时,该容器的容积为
(2012•南京二模)一块边长为10cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形作侧面,以它们的公共顶点p为顶点,加工成一个如图所示的正四棱锥形容器.当x=6cm时,该容器的容积为 一块边长为10cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积V与x的函数关系式,并求出函数的定义域.
一块边长为10cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积V与x的函数关系式,并求出函数的定义域.