题目内容
已知a>b>0,e1,e2分别是圆锥曲线| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
分析:根据e1,e2均大于0,故求m=e1+e2的范围可先求m平方的范围即求e12+e22+2e1e2的范围,而e12+e22=2,再根据a>b>0推断出 0<
<1,进而利用椭圆和双曲线的性质分别表示出e1和e2,进而求得e1e2的表达式,求得e1e2的范围,代入m2=e21+e22+2e1e2中,求得m2的范围.即可求解
| b |
| a |
解答:解:由题意得:
e1=
>0,e2=
>0
∵m=e1+e2
∴m2=e21+e22+2e1e2
即m2=2+2e1e2=2+2
=2+2
∵a>b>0
∴0<
<1
∴0<e1e2<1
即2<m2<4
即
<m<2
故答案为:(
,2)
e1=
| ||
| a |
| ||
| a |
∵m=e1+e2
∴m2=e21+e22+2e1e2
即m2=2+2e1e2=2+2
| ||
| a2 |
1-(
|
∵a>b>0
∴0<
| b |
| a |
∴0<e1e2<1
即2<m2<4
即
| 2 |
故答案为:(
| 2 |
点评:本题采用了转化思想,通过求解变量的平方从而解决了问题,是解决问题常用的手段,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
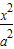 +
+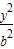 =1和
=1和 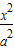 -
-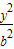 =1的离心率,则lg e1+lg e2的值( )
=1的离心率,则lg e1+lg e2的值( )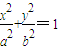 和
和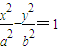 的离心率,设m=lne1+lne2,则m的取值范围是 .
的离心率,设m=lne1+lne2,则m的取值范围是 .