题目内容
已知a>b>0,e1,e2分别是圆锥曲线| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
分析:先根据a>b>0推断出0<
<1,进而利用椭圆和双曲线的性质分别表示出e1和e2,进而求得e1e2的表达式,求得e1e2的范围,代入m=lne1+lne2中求得m的范围.
| b |
| a |
解答:解:由条件得:0<
<1,e1=
,e2=
,
则e1•e2=
=
∴0<e1e2<1,
所以m=lge1+lge2=lg(e1e2)<0.
故答案为:(-∞,0)
| b |
| a |
| ||
| a |
| ||
| a |
则e1•e2=
| ||
| a2 |
1-(
|
∴0<e1e2<1,
所以m=lge1+lge2=lg(e1e2)<0.
故答案为:(-∞,0)
点评:本题主要考查了椭圆与双曲线的性质.考查了圆锥曲线中离心率的问题,一般是需要挖掘已知条件的信息求得a和c的关系.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
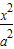 +
+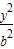 =1和
=1和 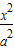 -
-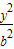 =1的离心率,则lg e1+lg e2的值( )
=1的离心率,则lg e1+lg e2的值( )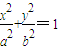 和
和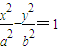 的离心率,设m=lne1+lne2,则m的取值范围是 .
的离心率,设m=lne1+lne2,则m的取值范围是 .