题目内容
在△ABC中,角A、B、C的对边分别是a、b、c,且满足(2a+c)cosB+bcosC=0
(1)求角B的大小
(2)若△ABC外接圆半径为
,求a+c的范围.
(1)求角B的大小
(2)若△ABC外接圆半径为
| 3 |
(1)∵(2a+c)cosB+bcosC=0,
∴由正弦定理,得(2sinA+sinC)cosB+sinBcosC=0.
即2sinAcosB+(sinCcosB+cosCsinB)=0
∵sin(C+B)=sinCcosB+sinBcosC,且sin(C+B)=sin(π-A)=sinA,
∴2sinAcosB+sinA=0,即sinA(2cosB+1)=0.
∵A∈(0,π),可得sinA>0,∴2cosB+1=0,得cosB=-
.
结合B是三角形的内角,可得B=
;
(2)∵ABC外接圆半径为R=
,∴b=2RsinB=2
×sin
=3.
由余弦定理,得b2=a2+c2-2accosB=9,
∴a2+c2-2accos
=9,化简得a2+c2+ac=9.
配方可得(a+c)2=9+ac,
∵ac≤[
(a+c)]2,∴(a+c)2≤9+
(a+c)2,解之得(a+c)2≤12,
因此a+c≤2
,当且仅当a=c时等号成立.
又∵△ABC中,a+c>b=3,
∴a+c的范围为(3,2
].
∴由正弦定理,得(2sinA+sinC)cosB+sinBcosC=0.
即2sinAcosB+(sinCcosB+cosCsinB)=0
∵sin(C+B)=sinCcosB+sinBcosC,且sin(C+B)=sin(π-A)=sinA,
∴2sinAcosB+sinA=0,即sinA(2cosB+1)=0.
∵A∈(0,π),可得sinA>0,∴2cosB+1=0,得cosB=-
| 1 |
| 2 |
结合B是三角形的内角,可得B=
| 2π |
| 3 |
(2)∵ABC外接圆半径为R=
| 3 |
| 3 |
| 2π |
| 3 |
由余弦定理,得b2=a2+c2-2accosB=9,
∴a2+c2-2accos
| 2π |
| 3 |
配方可得(a+c)2=9+ac,
∵ac≤[
| 1 |
| 2 |
| 1 |
| 4 |
因此a+c≤2
| 3 |
又∵△ABC中,a+c>b=3,
∴a+c的范围为(3,2
| 3 |

练习册系列答案
相关题目
 中,内角
中,内角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,已知
,已知 .
. ,
, ,求
,求 .
.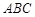 的面积是
的面积是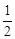 ,
,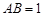 ,
,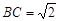 ,则
,则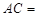 ( )
( )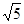
 ,那么b=
,那么b= B.
B. C.
C. D.
D.