题目内容
【题目】已知
（1）当
时，求函数
的单调区间；
（2）若函数有两个极值点
和
，
求证：b<2a
【答案】（1）（
，1）是减区间，（0，
）和（1，+∞）是增区间；（2）详见解析
【解析】
试题分析：（1）将
代入函数式，通过函数导数的正负得到函数的增减区间；（2）由题意可知
是方程
的根，依据根的分布规律可得
的不等式，从而得到
试题解析：（1）f‘（x）=2x-3+
=
（x＞0）， 2分
由f'（x）=0得x=
或x=1，．∴当x＞1或0＜x＜
时，f'（x）＞0，
当
＜x＜1时f'（x）＜0， 4分
∴（
，1）是函数f（x）的减区间，（0，
）和（1，+∞）是f（x）的增区间；．．5分
（2）∵函数f（x）有两个极值点x1，x2，∴f（x）=0在（0，+∞）有两个不同的解x1，x2，
．∵f（x）=ax+（b-1）+
=
， 6分
∴x1，x2是ax2+（b-1）x+1=0在（0，+∞）内的两个不同解，
设h（x）=ax2+（b-1）x+1，则该函数有两个零点x1，x2，
∵0＜x1＜2＜x2＜4，∴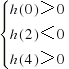
即
， 9分
∴
-4a＜b＜
-2a，即
-4a＜
-2a得a＞
， 11分
∴b＜
-2a＜4a-2a=2a，∴b＜2a得证；． 12分
练习册系列答案
阳光课堂同步练习系列答案
相关题目
