题目内容
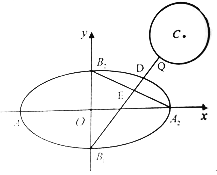
【题目】如图,已知椭圆![]() 的四个顶点分别为
的四个顶点分别为![]() ,左右焦点分别为
,左右焦点分别为![]() ,若圆
,若圆![]() :
:![]() 上有且只有一个点
上有且只有一个点![]() 满足
满足![]() .
.
(1)求圆![]() 的半径
的半径![]() ;
;
(2)若点![]() 为圆
为圆![]() 上的一个动点,直线
上的一个动点,直线![]() 交椭圆于点
交椭圆于点![]() ,交直线
,交直线![]() 于点
于点![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)半径为![]() ;(2)最大值为
;(2)最大值为![]() .
.
【解析】
试题分析:(1)先由已知条件,求出点![]() 的轨迹方程,再利用两圆相切,求出圆的半径,注意范围;(2)先设出直线
的轨迹方程,再利用两圆相切,求出圆的半径,注意范围;(2)先设出直线![]() 方程
方程![]() ,由直线与圆的位置关系,求出
,由直线与圆的位置关系,求出![]() 的范围,联立直线与圆的方程,求出
的范围,联立直线与圆的方程,求出![]() 点的横坐标, 直线
点的横坐标, 直线![]() 与直线
与直线![]() 的交点为
的交点为![]() 点,求出横坐标,利用相似得出
点,求出横坐标,利用相似得出 ![]() ,代入,再求出范围.
,代入,再求出范围.
试题解析:(1)依题意得,![]() ,设点
,设点![]() ,
,
由![]() 得:
得: ,化简得
,化简得![]() ,
,
∴点![]() 的轨迹是以点
的轨迹是以点![]() 为圆心,
为圆心,![]() 为半径的圆.
为半径的圆.
又∵点![]() 在圆
在圆![]() 上并且有且只有一个点
上并且有且只有一个点![]() ,即两圆相切,
,即两圆相切,
当两圆外切时,圆心距![]() ,成立;
,成立;
当两圆内切时,圆心距![]() ,不成立;
,不成立;
∴![]()
(2)设直线![]() 为
为![]() ,由
,由![]() ,得
,得![]() .
.
联立 消去
消去![]() 并整理得:
并整理得:![]() ,解得点
,解得点![]() 的横坐标为
的横坐标为![]() ,
,
把直线![]() 与直线
与直线![]() :
:![]() 联立解得点
联立解得点![]() 的横坐标为
的横坐标为![]() ,
,
∴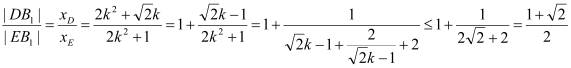
当且仅当![]() 时,取等号,
时,取等号,
∴![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目