题目内容
3.二次函数f(x)满足f(x+1)-f(x)=2x+3,且f(0)=2.(1)求f(x)的解析式;
(2)求f(x)在[-3,4]上的值域;
(3)若函数f(x+m)为偶函数,求f[f(m)]的值;
(4)求f(x)在[m,m+2]上的最小值.
分析 (1)设f(x)=ax2+bx+c,由f(0)=2得c=2,由f(x+1)-f(x)=2x+3,得2ax+a+b=2x+3,解方程组求出a,b的值,从而求出函数的解析式;
(2)求得二次函数的对称轴,比较区间的关系,即可得到最值,进而得到值域;
(3)由偶函数的性质可得关于y轴对称,可得m=-1,进而得到所求;
(4)对m讨论,注意对称轴和区间的关系,由单调性即可得到最小值.
解答 解:(1)设f(x)=ax2+bx+c,由f(0)=2得c=2,
故f(x)=ax2+bx+2.
因为f(x+1)-f(x)=2x+3,
所以a(x+1)2+b(x+1)+2-(ax2+bx+2)=2x+3.
即2ax+a+b=2x+3,
∴$\left\{\begin{array}{l}{2a=2}\\{a+b=3}\end{array}\right.$,解得:a=1,b=2,
∴f(x)=x2+2x+2;
(2)由f(x)=(x+1)2+1的对称轴为x=-1∈[-3,4],
即有x=-1取得最小值1,x=4取得最大值26,
则值域为[1,26];
(3)f(x)=(x+1)2+1,即有f(x+m)=(x+m+1)2+1,
由函数f(x+m)为偶函数,则m+1=0,解得m=-1.
即有f(f(m))=f(f(-1))=f(1)=5.
(4)当m+2≤-1即m≤-3时,[m,m+2]为减区间,
最小值为f(m+2)=m2+6m+10;
当m≤-1<m+2,即-3<m≤-1时,x=-1取得最小值1;
当-1<m<m+2,即m>-1时,区间[m,m+2]为增区间,
x=m取得最小值m2+2m+2.
综上可得m≤-3时,最小值为m2+6m+10;
-3<m≤-1时,最小值为1;
m>-1时,最小值为m2+2m+2.
点评 本题考查二次函数的解析式和值域及最值,考查分类讨论的思想方法,属于中档题.

| 男 | 女 | 总计 | |
| 爱好 | a | b | 73 |
| 不爱好 | c | 25 | |
| 总计 | 74 |
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
| A. | 36 | B. | 54 | C. | 72 | D. | 162 |
| A. | $\frac{\sqrt{6}}{8}$ | B. | $\frac{\sqrt{6}}{16}$ | C. | $\frac{\sqrt{3}}{8}$ | D. | $\frac{\sqrt{3}}{16}$ |
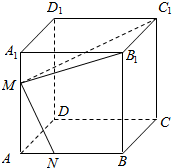 在正方体ABCD-A1B1C1D1中,M,N分别是A1A,AB上的点,若∠NMC1=90°,求证:NM⊥MB1.
在正方体ABCD-A1B1C1D1中,M,N分别是A1A,AB上的点,若∠NMC1=90°,求证:NM⊥MB1.