题目内容
已知椭圆 :
: (
( )的离心率
)的离心率 ,直线
,直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 ,以线段
,以线段 为直径作圆
为直径作圆 ,圆心为
,圆心为
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)当圆 与
与 轴相切的时候,求
轴相切的时候,求 的值;
的值;
(Ⅲ)若 为坐标原点,求
为坐标原点,求 面积的最大值。
面积的最大值。
 :
: (
( )的离心率
)的离心率 ,直线
,直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 ,以线段
,以线段 为直径作圆
为直径作圆 ,圆心为
,圆心为
(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)当圆
 与
与 轴相切的时候,求
轴相切的时候,求 的值;
的值;(Ⅲ)若
 为坐标原点,求
为坐标原点,求 面积的最大值。
面积的最大值。(Ⅰ) ;(Ⅱ)
;(Ⅱ) ;(Ⅲ)1.
;(Ⅲ)1.
 ;(Ⅱ)
;(Ⅱ) ;(Ⅲ)1.
;(Ⅲ)1.试题分析:(Ⅰ)∵椭圆
 的离心率
的离心率
∴
 ............................1分
............................1分解得
 ............................2分
............................2分故椭圆
 的方程为
的方程为 .................3分
.................3分(Ⅱ)联立方程可得:
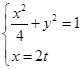 得
得 .........................5分
.........................5分即
 的坐标分别为
的坐标分别为 ........................6分
........................6分∵圆
 的直径为
的直径为 ,且与
,且与 轴相切
轴相切∴
 ,得
,得 (∵
(∵ )............8分
)............8分(Ⅲ)由(Ⅱ)可得,
 的面积
的面积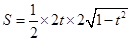 ......................9分
......................9分
=1...................10分
当且仅当
 即
即 时,等号成立.....................11分
时,等号成立.....................11分故
 的面积的最大值为1..................12分
的面积的最大值为1..................12分点评:充分理解圆C与y轴相切的含义是做本题的关键。要满足圆C与y轴相切也就是满足M点的纵坐标与横坐标相等。

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 的左、右两焦点分别为
的左、右两焦点分别为 ,点
,点 在椭圆上,
在椭圆上,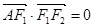 ,
, ,则椭圆的离心率
,则椭圆的离心率 等于 ( )
等于 ( )



 的焦点为
的焦点为 ,准线为
,准线为 ,过
,过 ;
; 的值.
的值. (a>0,b>0)的两个焦点,A和B是以O为圆心,以|OF1|为半径的圆与该左半椭圆的两个交点,且△F2AB是等边三角形,则椭圆的离心率为( )
(a>0,b>0)的两个焦点,A和B是以O为圆心,以|OF1|为半径的圆与该左半椭圆的两个交点,且△F2AB是等边三角形,则椭圆的离心率为( )


 -1
-1
 、
、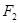 是双曲线
是双曲线 的两焦点,点
的两焦点,点 在该双曲线上,且
在该双曲线上,且 是等腰三角形,则
是等腰三角形,则



 的焦距为2,则
的焦距为2,则 .
.  与直线
与直线 围成的封闭图形的面积是( )
围成的封闭图形的面积是( )



 的焦点在
的焦点在 轴上,长轴长是短轴长的两倍,则m的值为 ( )
轴上,长轴长是短轴长的两倍,则m的值为 ( )



 与抛物线
与抛物线 的一个交点为M,
的一个交点为M, 为抛物线的焦点,若
为抛物线的焦点,若 ,则b的值为
,则b的值为 
