题目内容
【题目】已知点P是圆F1:(x﹣1)2+y2=8上任意一点,点F2与点F1关于原点对称,线段PF2的垂直平分线分别与PF1 , PF2交于M,N两点.
(1)求点M的轨迹C的方程;
(2)过点 ![]() 的动直线l与点M的轨迹C交于A,B两点,在y轴上是否存在定点Q,使以AB为直径的圆恒过这个点?若存在,求出点Q的坐标;若不存在,请说明理由.
的动直线l与点M的轨迹C交于A,B两点,在y轴上是否存在定点Q,使以AB为直径的圆恒过这个点?若存在,求出点Q的坐标;若不存在,请说明理由.
【答案】
(1)解:由题意得 ![]() ,
,
∴点M的轨迹C为以F1,F2为焦点的椭圆∵ ![]() ,
,
∴点M的轨迹C的方程为 ![]() .
.
(2)直线l的方程可设为 ![]() ,设A(x1,y1),B(x2,y2),
,设A(x1,y1),B(x2,y2),
联立 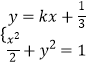 可得9(1+2k2)x2+12kx﹣16=0.
可得9(1+2k2)x2+12kx﹣16=0.
由求根公式化简整理得 ![]() ,
,
假设在y轴上是否存在定点Q(0,m),使以AB为直径的圆恒过这个点,则 ![]() 即
即 ![]() .
.
∵ ![]() ,
,
![]() =
= ![]() =
= ![]() =
= ![]() .
.
∴ ![]() 求得m=﹣1.
求得m=﹣1.
因此,在y轴上存在定点Q(0,﹣1),使以AB为直径的圆恒过这个点.
【解析】(1)根据中垂线的性质不难得到动点到两定点的距离之和为定值,且定值大于这两定点的距离,可得出动点的运动轨迹为椭圆,结合已知可得到轨迹方程,(2)将直线l的方程可设为 y = k x +![]() ,设出A、B两点的坐标,联立直线方程与椭圆方程,使用韦达定理得出A、B横坐标的和与积,假设在y轴上存在定点Q(0,m),则表示出
,设出A、B两点的坐标,联立直线方程与椭圆方程,使用韦达定理得出A、B横坐标的和与积,假设在y轴上存在定点Q(0,m),则表示出![]() ,
,![]() ,且
,且![]() ·
·![]() =0,可解得定点Q的坐标.
=0,可解得定点Q的坐标.

【题目】某种产品的质量以其质量指标衡量,并依据质量指标值划分等级如表:
质量指标值m | m<185 | 185≤m<205 | M≥205 |
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
(1)根据以上抽样调查的数据,能否认为该企业生产这种产品符合“一、二等品至少要占到全部产品的92%的规定”?
(2)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品的质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值X近似满足X~N(218,140),则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?