题目内容
已知椭圆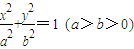 ,左右焦点分别为F1,F2,长轴的一个端点与短轴两个端点组成等边三角形,直线l经过点F2,倾斜角为45°,与椭圆交于A,B两点.
,左右焦点分别为F1,F2,长轴的一个端点与短轴两个端点组成等边三角形,直线l经过点F2,倾斜角为45°,与椭圆交于A,B两点.(1)若|F1F2|=2
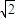 ,求椭圆方程;
,求椭圆方程;(2)对(1)中椭圆,求△ABF1的面积;
(3)M是椭圆上任意一点,若存在实数λ,μ,使得
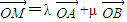 ,试确定λ,μ的关系式.
,试确定λ,μ的关系式.
【答案】分析:(1)利用长轴的一个端点与短轴两个端点组成等边三角形,|F1F2|=2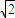 ,即可求椭圆方程;
,即可求椭圆方程;
(2)△ABF1的面积,可以以焦距长为底,A、B纵坐标差的绝对值为高进行求解;
(3)确定椭圆的右焦点F的坐标,设出直线AB所在直线方程为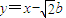 ,与椭圆方程联立,利用韦达定理及
,与椭圆方程联立,利用韦达定理及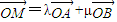 ,同时利用点A,B在椭圆上,即可求得λ,μ的关系式.
,同时利用点A,B在椭圆上,即可求得λ,μ的关系式.
解答:解:(1)由已知,可得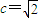 ,
,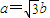 ,
,
∵a2=b2+c2,∴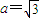 ,b=1,
,b=1,
∴椭圆方程为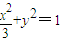 .
.
(2)设A(x1,y1),B(x2,y2),直线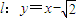 ,
,
代入椭圆方程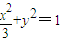 ,消去y可得
,消去y可得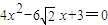 ,
,
∴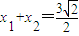 ,
,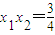 ,
,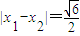 ,
,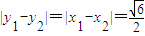 ,
,
∴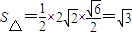 .
.
(3)由已知椭圆方程为x2+3y2=3b2①,右焦点F的坐标为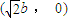 ,直线AB所在直线方程为
,直线AB所在直线方程为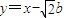 ②,
②,
由①②得: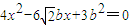 ,
,
设A(x1,y1),B(x2,y2),则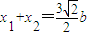 ,
,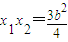 ,
,
设M(x,y),由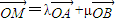 得,x=λx1+μx2,y=λy1+μy2,
得,x=λx1+μx2,y=λy1+μy2,
∵点M在椭圆上,∴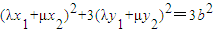 ,
,
整理得: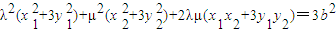 ,③
,③
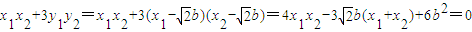 ④,
④,
又点A,B在椭圆上,故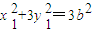 ⑤,
⑤,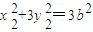 ⑥,
⑥,
将④⑤⑥代入③得λ2+μ2=1.
点评:本题考查椭圆的标准方程,考查三角形面积的计算,考查直线与椭圆的位置关系,联立方程,利用韦达定理是常用方法.
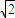 ,即可求椭圆方程;
,即可求椭圆方程;(2)△ABF1的面积,可以以焦距长为底,A、B纵坐标差的绝对值为高进行求解;
(3)确定椭圆的右焦点F的坐标,设出直线AB所在直线方程为
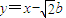 ,与椭圆方程联立,利用韦达定理及
,与椭圆方程联立,利用韦达定理及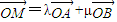 ,同时利用点A,B在椭圆上,即可求得λ,μ的关系式.
,同时利用点A,B在椭圆上,即可求得λ,μ的关系式.解答:解:(1)由已知,可得
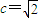 ,
,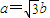 ,
,∵a2=b2+c2,∴
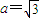 ,b=1,
,b=1,∴椭圆方程为
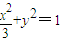 .
.(2)设A(x1,y1),B(x2,y2),直线
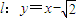 ,
,代入椭圆方程
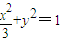 ,消去y可得
,消去y可得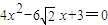 ,
,∴
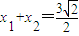 ,
,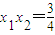 ,
,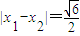 ,
,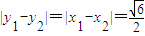 ,
,∴
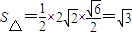 .
.(3)由已知椭圆方程为x2+3y2=3b2①,右焦点F的坐标为
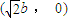 ,直线AB所在直线方程为
,直线AB所在直线方程为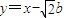 ②,
②,由①②得:
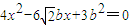 ,
,设A(x1,y1),B(x2,y2),则
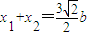 ,
,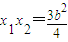 ,
,设M(x,y),由
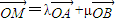 得,x=λx1+μx2,y=λy1+μy2,
得,x=λx1+μx2,y=λy1+μy2,∵点M在椭圆上,∴
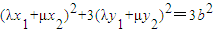 ,
,整理得:
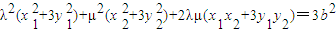 ,③
,③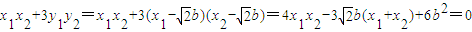 ④,
④,又点A,B在椭圆上,故
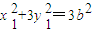 ⑤,
⑤,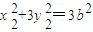 ⑥,
⑥,将④⑤⑥代入③得λ2+μ2=1.
点评:本题考查椭圆的标准方程,考查三角形面积的计算,考查直线与椭圆的位置关系,联立方程,利用韦达定理是常用方法.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目


 的左右焦点分别是
的左右焦点分别是 ,直线
,直线
 与椭圆
与椭圆 交于两点
交于两点 ,
, .当
.当 时,M恰为椭圆
时,M恰为椭圆 的周长为6.
的周长为6.
 与直线
与直线 分别相交于点
分别相交于点 ,
, ,问当
,问当
 为直径的圆被
为直径的圆被 轴截得的弦长是否为定值?若是,求出这个定值,
轴截得的弦长是否为定值?若是,求出这个定值, 的左右焦点分别是F1,F2,过右焦点F2且斜率为k的直线与椭圆交于A,B两点.
的左右焦点分别是F1,F2,过右焦点F2且斜率为k的直线与椭圆交于A,B两点.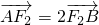 ,求k的值.
,求k的值.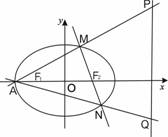 已知椭圆
已知椭圆 已知椭圆
已知椭圆 已知椭圆
已知椭圆