题目内容
已知椭圆

 的左右焦点分别是
的左右焦点分别是 ,直线
,直线
 与椭圆
与椭圆 交于两点
交于两点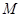 ,
, .当
.当 时,M恰为椭圆
时,M恰为椭圆 的上顶点,此时△
的上顶点,此时△ 的周长为6.
的周长为6.

(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设椭圆 的左顶点为A,直线
的左顶点为A,直线 与直线
与直线 分别相交于点
分别相交于点 ,
, ,问当
,问当
变化时,以线段 为直径的圆被
为直径的圆被 轴截得的弦长是否为定值?若是,求出这个定值,
轴截得的弦长是否为定值?若是,求出这个定值,
若不是,说明理由.
【答案】
(I)椭圆方程是: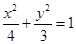 ;
;
(II)以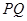 为直径的圆一定过右焦点
为直径的圆一定过右焦点 ,被
,被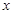 轴截得的弦长为定值6.
轴截得的弦长为定值6.
【解析】本试题主要是考查了直线与椭圆的 位置关系的综合运用。
(1)由题意可知三角形的周长和斜率用参数a,b,c表示出来得到结论。
(2)当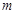 变化时,以线段
变化时,以线段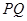 为直径的圆被
为直径的圆被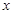 轴截得的弦长是否为定值,要分析m=0,m不为零的情况,结合直线与椭圆方程联立方程组,得到韦达定理和向量的关系来证明
轴截得的弦长是否为定值,要分析m=0,m不为零的情况,结合直线与椭圆方程联立方程组,得到韦达定理和向量的关系来证明

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 的左右焦点分别是F1,F2,过右焦点F2且斜率为k的直线与椭圆交于A,B两点.
的左右焦点分别是F1,F2,过右焦点F2且斜率为k的直线与椭圆交于A,B两点.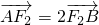 ,求k的值.
,求k的值. 已知椭圆
已知椭圆 已知椭圆
已知椭圆 已知椭圆
已知椭圆