题目内容
已知椭圆 的左右焦点分别是F1,F2,过右焦点F2且斜率为k的直线与椭圆交于A,B两点.
的左右焦点分别是F1,F2,过右焦点F2且斜率为k的直线与椭圆交于A,B两点.
(1)若k=1,求|AB|的长度、△ABF1的周长;
(2)若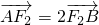 ,求k的值.
,求k的值.
解:(1)椭圆 中a=2,∴△ABF1的周长4a=8,
中a=2,∴△ABF1的周长4a=8,
由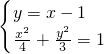 联立得7x2-8x-8=0
联立得7x2-8x-8=0
∴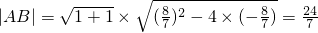
(2)设直线方程为y=k(x-1)代入椭圆方程,可得(3+4k2)x2-8k2x+4k2-12=0
设A(x1,y1),B(x2,y2),则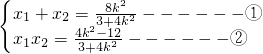
∵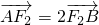 ,∴1-x1=2(x2-1)--③
,∴1-x1=2(x2-1)--③
由①③得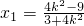 ,
,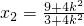
代入②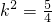 ,∴
,∴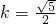
分析:(1)利用椭圆的定义,可求△ABF1的周长,直线方程与椭圆方程联立,利用韦达定理可求|AB|的长度;
(2)设直线方程为y=k(x-1)代入椭圆方程,利用韦达定理及向量知识,即可求k的值.
点评:本题考查椭圆的定义,考查直线与椭圆的位置关系,考查韦达定理的运用,考查向量知识,属于中档题.
 中a=2,∴△ABF1的周长4a=8,
中a=2,∴△ABF1的周长4a=8,由
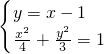 联立得7x2-8x-8=0
联立得7x2-8x-8=0∴
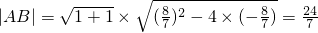
(2)设直线方程为y=k(x-1)代入椭圆方程,可得(3+4k2)x2-8k2x+4k2-12=0
设A(x1,y1),B(x2,y2),则
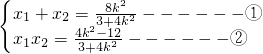
∵
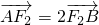 ,∴1-x1=2(x2-1)--③
,∴1-x1=2(x2-1)--③由①③得
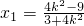 ,
,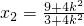
代入②
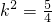 ,∴
,∴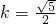
分析:(1)利用椭圆的定义,可求△ABF1的周长,直线方程与椭圆方程联立,利用韦达定理可求|AB|的长度;
(2)设直线方程为y=k(x-1)代入椭圆方程,利用韦达定理及向量知识,即可求k的值.
点评:本题考查椭圆的定义,考查直线与椭圆的位置关系,考查韦达定理的运用,考查向量知识,属于中档题.

练习册系列答案
相关题目


 的左右焦点分别是
的左右焦点分别是 ,直线
,直线
 与椭圆
与椭圆 交于两点
交于两点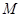 ,
, .当
.当 时,M恰为椭圆
时,M恰为椭圆 的周长为6.
的周长为6.
 与直线
与直线 分别相交于点
分别相交于点 ,
, ,问当
,问当
 为直径的圆被
为直径的圆被 轴截得的弦长是否为定值?若是,求出这个定值,
轴截得的弦长是否为定值?若是,求出这个定值, 已知椭圆
已知椭圆 已知椭圆
已知椭圆 已知椭圆
已知椭圆