题目内容
10．对于集合A={x|0≤x≤2}，B={y|0≤y≤3}，则由下列图形给出的对应f中，能构成从A到B的函数的是（ ）| A． |  | B． |  | C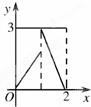． |  | D． |  |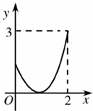
分析 直接根据函数的定义，逐个考察各选项便可得出结果．
解答 解：根据函数的定义，逐个考察各选项：
对于A：不能构成，因为集合A中有一部分元素（靠近x=2）并没有函数值，所以符合函数定义；
对于B：不能构成，因为集合A中的一个元素（如x=2）与集合B中的两个元素对应，不符合函数定义；
对于C：不能构成，因为集合A中的一个元素（如x=1）与集合B中的两个元素对应，不符合函数定义；
对于D：能够构成，因为集合A中的每个元素都只与集合B中某一个元素对应，符合函数定义．
故选D．
点评 本题主要考查了函数的概念，以及运用图象判断变量之间是否具有函数关系，属于基础题．
练习册系列答案
精英口算卡系列答案
相关题目
某单位用铁丝制作如图所示框架，框架的下部是边长分别为x、y（单位：米）的矩形，上部是一个半圆形，要求框架所围成的总面积为8m2
18．已知曲线y=x3+ax+b在x=1处的切线方程是y=2x+1，则实数b为（ ）
| A． | 1 | B． | -3 | C． | 3 | D． | -1 |
15．探究函数$f（x）=x+\frac{4}{x}，x∈（0，+∞）$的最小值，并确定取得最小值时x的值．列表如下：
请观察表中y值随x值变化的特点，完成以下的问题．
函数$f（x）=x+\frac{4}{x}（x＞0）$在区间（0，2）上递减；
函数$f（x）=x+\frac{4}{x}（x＞0）$在区间[2，+∞）上递增．
当x=2时，y最小=4
（1）用定义法证明：函数$f（x）=x+\frac{4}{x}（x＞0）$在区间（0，2）递减．
（2）思考：函数$f（x）=x+\frac{4}{x}（x＜0）$时，有最值吗？是最大值还是最小值？此时x为何值？（直接回答结果，不需证明）
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.002 | 4.04 | 4.3 | 5 | 4.8 | 7.57 | … |
函数$f（x）=x+\frac{4}{x}（x＞0）$在区间（0，2）上递减；
函数$f（x）=x+\frac{4}{x}（x＞0）$在区间[2，+∞）上递增．
当x=2时，y最小=4
（1）用定义法证明：函数$f（x）=x+\frac{4}{x}（x＞0）$在区间（0，2）递减．
（2）思考：函数$f（x）=x+\frac{4}{x}（x＜0）$时，有最值吗？是最大值还是最小值？此时x为何值？（直接回答结果，不需证明）