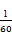题目内容
某示范性高中的校长推荐甲、乙、丙三名学生参加某大学自主招生考核测试,在本次考核中只有合格和优秀两个等级.若考核为合格,授予10分降分资格;考核为优秀, 授予20分降分资格.假设甲、乙、丙考核为优秀的概率分别为 、
、 、
、 ,他们考核所得的等级相互独立.
,他们考核所得的等级相互独立.
(1)求在这次考核中,甲、乙、丙三名学生至少有一名考核为优秀的概率;
(2)记在这次考核中甲、乙、丙三名学生所得降分之和为随机变量ξ,求随机变量ξ的分布列和数学期望.
 、
、 、
、 ,他们考核所得的等级相互独立.
,他们考核所得的等级相互独立.(1)求在这次考核中,甲、乙、丙三名学生至少有一名考核为优秀的概率;
(2)记在这次考核中甲、乙、丙三名学生所得降分之和为随机变量ξ,求随机变量ξ的分布列和数学期望.
(1)记“甲考核为优秀”为事件A,“乙考核为优秀”为事件B,“丙考核为优秀”为事件C,“甲、乙、丙至少有一名考核为优秀”为事件E.
则事件A、B、C是相互独立事件,事件

 与事件E是对立事件,于是
与事件E是对立事件,于是
P(E)=1-P(

 )=1-(1-
)=1-(1- )(1-
)(1- )(1-
)(1- )=
)= .
.
(2)ξ的所有可能取值为30,40,50,60.
P(ξ=30)=P(

 )=(1-
)=(1- )(1-
)(1- )(1-
)(1- )=
)= ,
,
P(ξ=40)=P(A
 )+P(
)+P( B
B )+P(
)+P(
 C)=
C)= ,
,
P(ξ=50)=P(AB )+P(A
)+P(A C)+P(
C)+P( BC)=
BC)= ,
,
P(ξ=60)=P(ABC)= .
.
所以ξ的分布列为
∴E(ξ)=30× +40×
+40× +50×
+50× +60×
+60× =
= .
.
则事件A、B、C是相互独立事件,事件


 与事件E是对立事件,于是
与事件E是对立事件,于是P(E)=1-P(


 )=1-(1-
)=1-(1- )(1-
)(1- )(1-
)(1- )=
)= .
.(2)ξ的所有可能取值为30,40,50,60.
P(ξ=30)=P(


 )=(1-
)=(1- )(1-
)(1- )(1-
)(1- )=
)= ,
,P(ξ=40)=P(A

 )+P(
)+P( B
B )+P(
)+P(
 C)=
C)= ,
,P(ξ=50)=P(AB
 )+P(A
)+P(A C)+P(
C)+P( BC)=
BC)= ,
,P(ξ=60)=P(ABC)=
 .
.所以ξ的分布列为
| ξ | 30 | 40 | 50 | 60 |
| P |  |  |  |  |
∴E(ξ)=30×
 +40×
+40× +50×
+50× +60×
+60× =
= .
.
练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 第2组
第2组 第3组
第3组 第4组
第4组 第5组
第5组 得到的频率分布直方图如图所示,
得到的频率分布直方图如图所示,

 这2n个连续正整数分成A,B两组,每组n个数,A组最小数为
这2n个连续正整数分成A,B两组,每组n个数,A组最小数为 ,最大数为
,最大数为 ;B组最小数为
;B组最小数为 ,最大数为
,最大数为 ,记
,记
 时,求
时,求 的分布列和数学期望;
的分布列和数学期望; 的取值恰好相等,求事件C发生的概率
的取值恰好相等,求事件C发生的概率 ;
; 表示C的对立事件,判断
表示C的对立事件,判断 的大小关系,并说明理由。
的大小关系,并说明理由。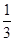



 ,乙、丙去北京旅游的概率分别为
,乙、丙去北京旅游的概率分别为 ,
, ,假定三人的行动相互之间没有影响,那么这段时间内至少有1人去北京旅游的概率为( )
,假定三人的行动相互之间没有影响,那么这段时间内至少有1人去北京旅游的概率为( )