题目内容
(满分14分)随机将 这2n个连续正整数分成A,B两组,每组n个数,A组最小数为
这2n个连续正整数分成A,B两组,每组n个数,A组最小数为 ,最大数为
,最大数为 ;B组最小数为
;B组最小数为 ,最大数为
,最大数为 ,记
,记
(1)当 时,求
时,求 的分布列和数学期望;
的分布列和数学期望;
(2)令C表示事件 与
与 的取值恰好相等,求事件C发生的概率
的取值恰好相等,求事件C发生的概率 ;
;
(3)对(2)中的事件C, 表示C的对立事件,判断
表示C的对立事件,判断 和
和 的大小关系,并说明理由。
的大小关系,并说明理由。
 这2n个连续正整数分成A,B两组,每组n个数,A组最小数为
这2n个连续正整数分成A,B两组,每组n个数,A组最小数为 ,最大数为
,最大数为 ;B组最小数为
;B组最小数为 ,最大数为
,最大数为 ,记
,记
(1)当
 时,求
时,求 的分布列和数学期望;
的分布列和数学期望;(2)令C表示事件
 与
与 的取值恰好相等,求事件C发生的概率
的取值恰好相等,求事件C发生的概率 ;
;(3)对(2)中的事件C,
 表示C的对立事件,判断
表示C的对立事件,判断 和
和 的大小关系,并说明理由。
的大小关系,并说明理由。(1)
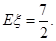 (2)当
(2)当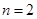 时,
时,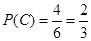 ,当
,当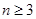 时
时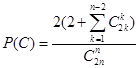
(3)当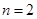 时,
时,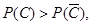 当
当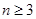 时,
时,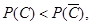
 | 2 | 3 | 4 | 5 |
| P | 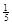 | 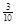 | 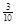 | 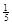 |
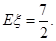 (2)当
(2)当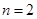 时,
时,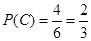 ,当
,当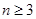 时
时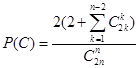
(3)当
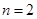 时,
时,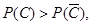 当
当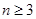 时,
时,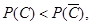
试题分析:(1)当
 时,将6个正整数平均分成A,B两组,不同的分组方法共有
时,将6个正整数平均分成A,B两组,不同的分组方法共有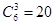 种,
种, 所有可能值为2,3,4,5.对应组数分别为4,6,6,4,对应概率为
所有可能值为2,3,4,5.对应组数分别为4,6,6,4,对应概率为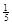 ,
,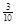 ,
,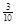 ,
,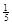 ,
,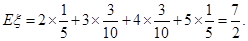 (2)
(2) 和
和 恰好相等的所有可能值为
恰好相等的所有可能值为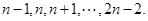 当
当 和
和 恰好相等且等于
恰好相等且等于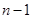 时,不同的分组方法有2种;当
时,不同的分组方法有2种;当 和
和 恰好相等且等于
恰好相等且等于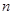 时,不同的分组方法有2种;当
时,不同的分组方法有2种;当 和
和 恰好相等且等于
恰好相等且等于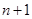 时,不同的分组方法有2
时,不同的分组方法有2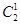 种;当
种;当 和
和 恰好相等且等于
恰好相等且等于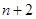 时,不同的分组方法有2
时,不同的分组方法有2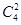 种;以此类推:
种;以此类推: 和
和 恰好相等且等于
恰好相等且等于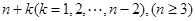 时,不同的分组方法有2
时,不同的分组方法有2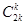 种;所以当
种;所以当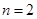 时,
时,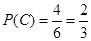
当
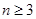 时
时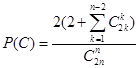 (3)先归纳:当
(3)先归纳:当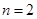 时,
时,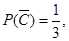 因此
因此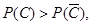 当
当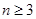 时,
时,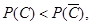 即证当
即证当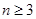 时
时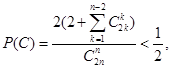
 ,这可用数学归纳法证明. 当
,这可用数学归纳法证明. 当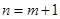 时,
时,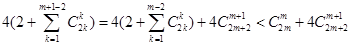 ,利用阶乘作差
,利用阶乘作差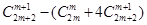 可得大小.
可得大小.试题解析:(1)当
 时,
时, 所有可能值为2,3,4,5.将6个正整数平均分成A,B两组,不同的分组方法共有
所有可能值为2,3,4,5.将6个正整数平均分成A,B两组,不同的分组方法共有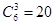 种,所以
种,所以 的分布列为
的分布列为 | 2 | 3 | 4 | 5 |
| P | 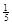 | 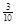 | 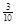 | 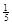 |
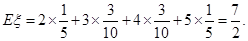
(2)
 和
和 恰好相等的所有可能值为
恰好相等的所有可能值为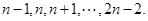
又
 和
和 恰好相等且等于
恰好相等且等于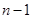 时,不同的分组方法有2种;
时,不同的分组方法有2种; 和
和 恰好相等且等于
恰好相等且等于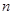 时,不同的分组方法有2种;
时,不同的分组方法有2种; 和
和 恰好相等且等于
恰好相等且等于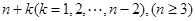 时,不同的分组方法有2
时,不同的分组方法有2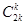 种;
种;所以当
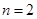 时,
时,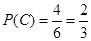
当
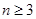 时
时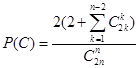
(3)由(2)当
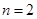 时,
时,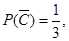 因此
因此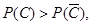
而当
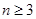 时,
时,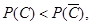 理由如下:
理由如下: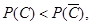 等价于
等价于 ①
①用数学归纳法来证明:
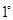 当
当 时,①式左边
时,①式左边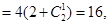 ①式右边
①式右边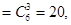 所以①式成立
所以①式成立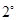 假设
假设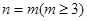 时①式成立,即
时①式成立,即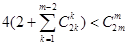 成立
成立那么,当
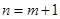 时,①式左边
时,①式左边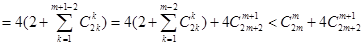
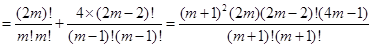
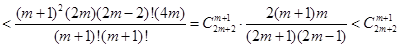 =①式右边
=①式右边即当
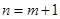 时①式也成立
时①式也成立综合
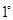
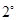 得,对于
得,对于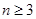 的所有正整数,都有
的所有正整数,都有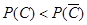 成立
成立
练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 、
、 ,他们考核所得的等级相互独立.
,他们考核所得的等级相互独立. 、
、 、
、 、
、 、
、 中任取两个不同的字母,则取到字母
中任取两个不同的字母,则取到字母 中随机选取一个数为
中随机选取一个数为 从
从 中随机选取一个数
中随机选取一个数 ,则
,则 的概率是( )
的概率是( )


