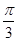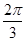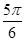题目内容
(本题满分13分)已知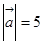 ,
,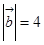 ,且
,且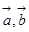 夹角为
夹角为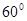 ,
,
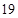
(1)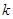 为何值时,
为何值时, 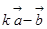 与
与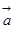 垂直?
垂直?
(2)在(1)的条件下,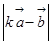 是否为某种最值?请简要叙述你的理由.
是否为某种最值?请简要叙述你的理由.
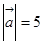 ,
,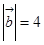 ,且
,且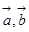 夹角为
夹角为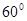 ,
,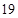
(1)
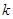 为何值时,
为何值时, 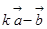 与
与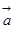 垂直?
垂直?(2)在(1)的条件下,
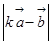 是否为某种最值?请简要叙述你的理由.
是否为某种最值?请简要叙述你的理由.简解:(1)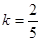
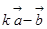
(2)在(1)的条件下,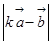 取最小值.实际上:
取最小值.实际上: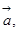
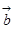 平移至相同起始点后,
平移至相同起始点后,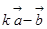 与
与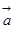 垂直时,由向量减法几何意义
垂直时,由向量减法几何意义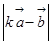 表示
表示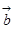 终点到
终点到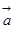 所在直线的距离,点到直线距离最短.也可借助函数证得最小值.
所在直线的距离,点到直线距离最短.也可借助函数证得最小值.
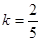
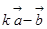
(2)在(1)的条件下,
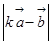 取最小值.实际上:
取最小值.实际上: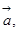
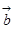 平移至相同起始点后,
平移至相同起始点后,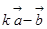 与
与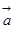 垂直时,由向量减法几何意义
垂直时,由向量减法几何意义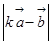 表示
表示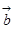 终点到
终点到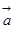 所在直线的距离,点到直线距离最短.也可借助函数证得最小值.
所在直线的距离,点到直线距离最短.也可借助函数证得最小值.(1)若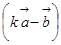
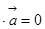 ,则
,则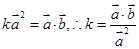 计算出k值.
计算出k值.
(2)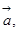
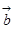 平移至相同起始点后,
平移至相同起始点后,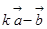 与
与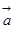 垂直时,由向量减法几何意义
垂直时,由向量减法几何意义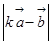 表示
表示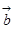 终点到
终点到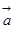 所在直线的距离,点到直线距离最短.也可借助函数证得最小值.
所在直线的距离,点到直线距离最短.也可借助函数证得最小值.
简解:(1)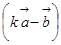
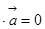
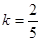
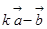
(2)在(1)的条件下,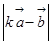 取最小值.
取最小值.
实际上: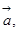
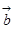 平移至相同起始点后,
平移至相同起始点后,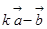 与
与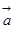 垂直时,由向量减法几何意义
垂直时,由向量减法几何意义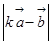 表示
表示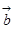 终点到
终点到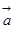 所在直线的距离,点到直线距离最短.也可借助函数证得最小值.
所在直线的距离,点到直线距离最短.也可借助函数证得最小值.
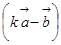
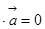 ,则
,则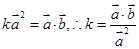 计算出k值.
计算出k值.(2)
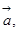
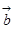 平移至相同起始点后,
平移至相同起始点后,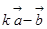 与
与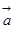 垂直时,由向量减法几何意义
垂直时,由向量减法几何意义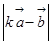 表示
表示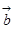 终点到
终点到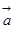 所在直线的距离,点到直线距离最短.也可借助函数证得最小值.
所在直线的距离,点到直线距离最短.也可借助函数证得最小值.简解:(1)
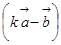
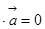
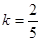
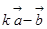
(2)在(1)的条件下,
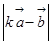 取最小值.
取最小值.实际上:
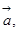
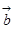 平移至相同起始点后,
平移至相同起始点后,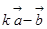 与
与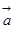 垂直时,由向量减法几何意义
垂直时,由向量减法几何意义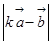 表示
表示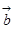 终点到
终点到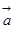 所在直线的距离,点到直线距离最短.也可借助函数证得最小值.
所在直线的距离,点到直线距离最短.也可借助函数证得最小值.
练习册系列答案
相关题目
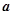 ,
,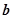 满足
满足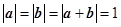 ,则向量
,则向量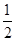
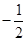
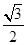
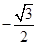
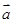 与
与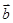 的夹角为60o,且满足
的夹角为60o,且满足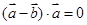 ,若
,若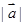 =1,则
=1,则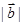 =( )
=( )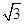
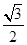
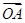 +
+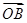 +
+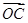 = m
= m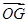 ,则实数m= .
,则实数m= .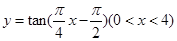 的图象与
的图象与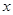 轴交于
轴交于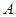 点,过点
点,过点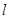 与函数的图象交于
与函数的图象交于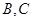 两点, 则
两点, 则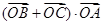
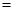 ( )
( ) 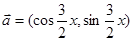 ,
,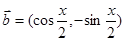 ,且
,且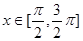
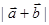 的取值范围;
的取值范围;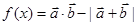 的最小值,并求此时x的值
的最小值,并求此时x的值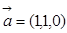 ,
,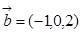 ,且
,且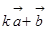 与
与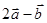 互相垂直,则k等于 _______________________(用分数作答)
互相垂直,则k等于 _______________________(用分数作答)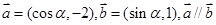 则
则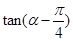 等于( )
等于( ) 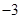

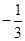
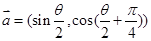 ,
,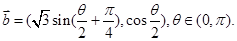 并且满足
并且满足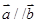 .则
.则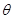 的值为( )
的值为( )