题目内容
8.已知实数x,y满足条件$\left\{\begin{array}{l}{x-y+5≥0}\\{x+y≥0}\\{x≤3}\end{array}\right.$,z=x+yi(i为虚数单位),则|z-1+2i|的最小值是( )| A. | $\frac{\sqrt{2}}{2}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | $\sqrt{5}$ |
分析 本题本质是线性规划问题,先作出不等式组对应的区域,再利用复数的几何意义将|z-1+2i|的最大值和最小值转化成定点与区域中的点的距离最大与最小的问题利用图形求解.
解答 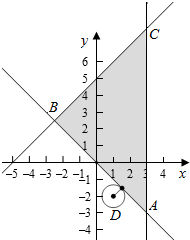 解:如图,作出$\left\{\begin{array}{l}x-y+5≥0\\ x+y≥0\\ x≤3\end{array}\right.$对应的区域,由于z=x+yi(i为虚数单位),
解:如图,作出$\left\{\begin{array}{l}x-y+5≥0\\ x+y≥0\\ x≤3\end{array}\right.$对应的区域,由于z=x+yi(i为虚数单位),
所以|z-1+2i|表示点(x,y)与D(1,-2)两点之间的距离,
由图象可知|z-1+2i|的最小值为D到直线x+y=0的距离,
即d=$\frac{|1-2|}{\sqrt{2}}=\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
故选:A.
点评 本题考查一定点与区域中的一动点距离最值的问题,利用线性规划的知识进行求解是解决本题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
19.已知命题p:?x∈R,x2+2x+2>0,则¬p是( )
| A. | ?x0∈R,x02+2x0+2<0 | B. | ?x∈R,x2+2x+2<0 | ||
| C. | ?x0∈R,x02+2x0+2≤0 | D. | ?x∈R,x2+2x+2≤0 |
3.若$\frac{sinθ}{{\sqrt{1+{{cot}^2}θ}}}-\frac{cosθ}{{\sqrt{1+{{tan}^2}θ}}}=-1$$(θ≠\frac{kπ}{2},k∈Z)$,则θ是第几象限角( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
13.已知a,b均为正数,$\frac{1}{a}+\frac{4}{b}=3$,则使a+b≥c恒成立的c的取值范围是( )
| A. | (-∞,1] | B. | (-∞,2] | C. | (-∞,3] | D. | (-∞,9] |