题目内容
12.已知正项等比数列{an}的前n项和为Sn,且a3=$\frac{1}{4}$,S3=$\frac{7}{4}$,数列{bn}的前n项和Tn满足Tn+1-bn=2,n∈N*,且b1=1.(1)求b2,b3,b4的值和数列{an}的通项公式;
(2)试探究bn与bn+6的关系,并求$\sum_{i=1}^{6n}$aibi(其中n∈N*).
分析 (1)由数列{bn}的前n项和Tn满足Tn+1-bn=2,n∈N*,且b1=1.分别取n=1,2,3,可得b2,b3,b4.设正项等比数列{an}的公比为q>0.由a3=$\frac{1}{4}$,S3=$\frac{7}{4}$,可得${a}_{1}{q}^{2}$=$\frac{1}{4}$,${a}_{1}+{a}_{1}q+{a}_{1}{q}^{2}$=$\frac{7}{4}$,解出即可.
(2)由(1)可得:b5=-2,b6=-1,b7=1,b8=2,…,可得bn+6=bn.计算$\sum_{i=1}^{6}{a}_{i}{b}_{i}$=$\frac{63}{32}$.可得$\sum_{i=1}^{6n}$aibi=$\frac{63}{32}[1+(\frac{1}{2})^{6}+(\frac{1}{2})^{12}+$…+$(\frac{1}{2})^{6n-6}]$.
解答 解:(1)∵数列{bn}的前n项和Tn满足Tn+1-bn=2,n∈N*,且b1=1.
分别取n=1,2,3,可得b2=2,b3=1,b4=-1.
设正项等比数列{an}的公比为q>0.
∵a3=$\frac{1}{4}$,S3=$\frac{7}{4}$,
∴${a}_{1}{q}^{2}$=$\frac{1}{4}$,${a}_{1}+{a}_{1}q+{a}_{1}{q}^{2}$=$\frac{7}{4}$,
解得a1=1,q=$\frac{1}{2}$.
∴${a}_{n}=(\frac{1}{2})^{n-1}$.
(2)由(1)可得:b5=-2,b6=-1,b7=1,b8=2,…,
可得bn+6=bn.
∵$\sum_{i=1}^{6}{a}_{i}{b}_{i}$=$1×(\frac{1}{2})^{0}$+$2×(\frac{1}{2})^{1}$+$1×(\frac{1}{2})^{2}$-$(\frac{1}{2})^{3}$-2×$(\frac{1}{2})^{4}$-$(\frac{1}{2})^{5}$=$\frac{63}{32}$.
∴$\sum_{i=1}^{6n}$aibi=$\frac{63}{32}[1+(\frac{1}{2})^{6}+(\frac{1}{2})^{12}+$…+$(\frac{1}{2})^{6n-6}]$
=$\frac{63}{32}$×$\frac{1-(\frac{1}{64})^{n}}{1-\frac{1}{64}}$=$2[1-(\frac{1}{64})^{n}]$.
点评 本题考查了等比数列的定义通项公式及其前n项和公式、数列的周期性,考查了变形能力与计算能力,属于中档题.

| A. | x2+(y+1)2=1 | B. | x2+(y+$\sqrt{3}$)2=3 | C. | x2+(y+$\frac{\sqrt{3}}{2}$)2=$\frac{3}{4}$ | D. | x2+(y+2)2=4 |
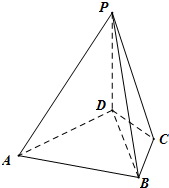 如图,四棱锥P-ABCD中,PD⊥平面ABCD,△ABD是边长为3的正三角形,BC=CD=$\sqrt{3}$,PD=4.
如图,四棱锥P-ABCD中,PD⊥平面ABCD,△ABD是边长为3的正三角形,BC=CD=$\sqrt{3}$,PD=4.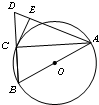 如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=8,DC=4,则DE=2.
如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=8,DC=4,则DE=2. 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点. 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.