题目内容
【题目】已知Sn是正项数列{an}的前n项和，且Sn= 
an2+ 
an﹣ 
（1）求数列{an}的通项公式；
（2）若an=2nbn ， 求数列{bn}的前n项和．
【答案】
（1）解：∵Sn= 
+ 
an﹣ 
，
∴Sn﹣1= 
+ an﹣1﹣ ，
∴an=Sn﹣Sn﹣1= （ ﹣ ）+ （an﹣an﹣1）（n≥2），
∵正项数列{an}，
∴an﹣an﹣1=2，易得a1=3，
∴an=2n+1
（2）解：∵an=2nbn
∴bn= 
= 
∴Tn= 
+ 
+…+
Tn= 
+ +…+ 
+
上面两式相减得，
Tn= 
+ 
+ 
+…+ 
﹣ 
= +2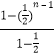 
﹣ ，
∴Tn=5﹣（2n+5） 
【解析】（1）运用an= 
即可求出an；（2）运用数列的求和方法：错位相减法，即可求出数列{bn}的前n项和．
【考点精析】认真审题，首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系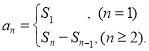
)．
练习册系列答案
优百分课时互动系列答案
相关题目
