��Ŀ����
����Ŀ���ס��������̳���ͬһ����Ʒ��չ��������Թ������Ʒ�Ĺ˿������̳��Ľ�����������:
���̳�:�˿�ת����ͼ��ʾԲ�̣���ָ��ָ����Ӱ����(ͼ��������Ӱ���־�Ϊ���Σ���ÿ������Բ�ĽǾ�Ϊ![]() ���߽���Բ���)��Ϊ�н���
���߽���Բ���)��Ϊ�н���
���̳�:��װ��2������2�������2������ĺ�����һ��������1��(��Щ�����ɫ����ȫ��ͬ)�����Ǻ���ĸ�����![]() �����Ӻ�����һ��������2������������2����ͬ��ɫ����Ϊ�н�.
�����Ӻ�����һ��������2������������2����ͬ��ɫ����Ϊ�н�.

������ʵ��![]() ��ֵ��
��ֵ��
�������ʣ��������Ʒ�Ĺ˿����ļ��̳��н��Ŀ����Դ���˵������.
���𰸡�����![]() ;���˿��ڼ��̳��н��Ŀ����Դ�.
;���˿��ڼ��̳��н��Ŀ����Դ�.
���������������������������¼��ĸ��ʹ�ʽ,�������![]() ��ֵ��������˿�ȥ���̳�ת��Բ�̣�ָ��ָ����Ӱ����Ϊ�¼�
��ֵ��������˿�ȥ���̳�ת��Բ�̣�ָ��ָ����Ӱ����Ϊ�¼�![]() �����ü��θ�������˿�ȥ���̳��н��ĸ��ʣ���˿�ȥ���̳�һ������������ͬ��ɫ����Ϊ�¼�
�����ü��θ�������˿�ȥ���̳��н��ĸ��ʣ���˿�ȥ���̳�һ������������ͬ��ɫ����Ϊ�¼�![]() �����õȿ����¼����ʼ��㹫ʽ����˿�ȥ���̳��н��ĸ��ʣ��ɴ�������˿��ڼ��̳��н��Ŀ����Դ�
�����õȿ����¼����ʼ��㹫ʽ����˿�ȥ���̳��н��ĸ��ʣ��ɴ�������˿��ڼ��̳��н��Ŀ����Դ�
�������������������¼��ĸ��ʹ�ʽ�� ![]() �����
�����![]() .
.
������˿�ȥ���̳�ת��Բ�̣�ָ��ָ����Ӱ����Ϊ�¼�![]() �������ȫ��������ɵ�����ΪԲ�̣�
�������ȫ��������ɵ�����ΪԲ�̣�
���Ϊ![]() ��
��![]() ΪԲ�̵İ뾶������Ӱ��������Ϊ
ΪԲ�̵İ뾶������Ӱ��������Ϊ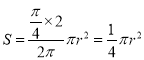 .
.
���ɼ��θ��ͣ��� .
.
��˿�ȥ���̳�һ������������ͬ��ɫ����Ϊ�¼�![]() ����2������Ϊ��1����2��2������Ϊ��1����2��2������Ϊ��1����2.
����2��������1����2��2��������1����2��2��������1����2.
��Ӻ�����һ��������2��һ�п��ܵĽ���У���1����2��������1����1��������1����2��������1����1��������1����2��������2����1��������2����2��������2����1��������2����2��������1����1��������1����2��������2����1��������2����2��������1����2���ȹ�15�֣�
������������2����ͬ��ɫ�����У���1����2��������1����2��������1����2���ȹ�3�֣�
���ɹŵ���ͣ���![]() .
.
��Ϊ![]() �����Թ˿��ڼ��̳��н��Ŀ����Դ�.
�����Թ˿��ڼ��̳��н��Ŀ����Դ�.

 �Ķ��쳵ϵ�д�
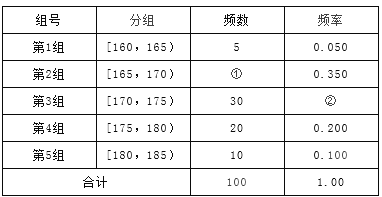
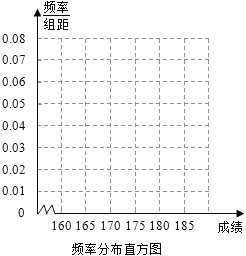
�Ķ��쳵ϵ�д�����Ŀ������������![]() ����γ���ÿ��γ����������ͺͱ��������ͺţ�ij�µIJ������±�(��λ����)�������÷ֲ�����ķ���������������Ľγ��г�ȡ50����������A��γ�10����
����γ���ÿ��γ����������ͺͱ��������ͺţ�ij�µIJ������±�(��λ����)�������÷ֲ�����ķ���������������Ľγ��г�ȡ50����������A��γ�10����
�γ� | �γ� | �γ� | |
������ | 100 | 150 |
|
���� | 300 | 450 | 600 |
(1)��![]() ��ֵ��
��ֵ��
(2)�÷ֲ�����ķ�����![]() ��γ��г�ȡһ������Ϊ5��������������������һ�����壬������ȡ
��γ��г�ȡһ������Ϊ5��������������������һ�����壬������ȡ
2������������1�������ͽγ��ĸ��ʣ�
(3)����������ķ�����![]() �������ͽγ��г�ȡ8������������ǵĵ÷����£�
�������ͽγ��г�ȡ8������������ǵĵ÷����£�![]() . ����8���γ��ĵ÷ֿ���һ�����壬������ȡһ�����������������ƽ����֮��ľ��� ֵ������
. ����8���γ��ĵ÷ֿ���һ�����壬������ȡһ�����������������ƽ����֮��ľ��� ֵ������![]() �ĸ��ʣ�
�ĸ��ʣ�