题目内容
【题目】设{an}是等差数列，{bn}是各项都为正数的等比数列，且a1=b1=1，a3+b5=21，a5+b3=13．
（1）求{an}、{bn}的通项公式；
（2）求数列 
的前n项和Sn ．
【答案】
（1）解：设{an}的公差为d，{bn}的公比为q，则依题意有q＞0且 
解得d=2，q=2．
所以an=1+（n﹣1）d=2n﹣1，bn=qn﹣1=2n﹣1．
（2）解： 
，
，①
Sn= 
，②
①﹣②得 Sn=1+2（ + 
+…+ 
）﹣ 
，
则 
= 
= 
= 
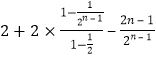【解析】（1）设{an}的公差为d，{bn}的公比为q，根据等比数列和等差数列的通项公式，联立方程求得d和q，进而可得{an}、{bn}的通项公式．（2）数列 
的通项公式由等差和等比数列构成，进而可用错位相减法求得前n项和Sn ．
练习册系列答案
相关题目
