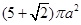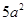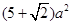题目内容
平行六面体ABCD-A1B1C1D1中,AB=4,AD=3,AA1=5,∠BAD=90°,
∠BAA1=∠DAA1=60°,则AC1=( )
| A.85 | B. | C.5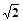 | D.50 |
B
解析试题分析:解:如图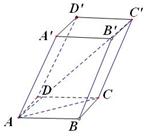
连接AC,∵AB=4,AD=3,∠BAD=90°,∴AC=5,根据cos∠A‘AB=cos∠A’AC•cos∠CAB,即 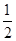 =cos∠A‘AC•
=cos∠A‘AC•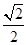 ∴∠A'AC=45°则∠C’CA=135°,而AC=5,AA‘=5,根据余弦定理得AC’=
∴∠A'AC=45°则∠C’CA=135°,而AC=5,AA‘=5,根据余弦定理得AC’= 故答案为:B
故答案为:B
考点:空间中两点的距离
点评:本题主要考查了体对角线的求解,以及余弦定理的应用,同时考查了空间想象能力,计算推理的能力,属于中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
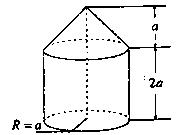
已知几何体M的正视图是一个面积为2 的半圆,俯视图是正三角形,那么这个几何体的表面积和体积为
的半圆,俯视图是正三角形,那么这个几何体的表面积和体积为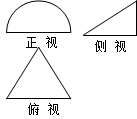
A.6 和 和  | B.6 +4 +4 和 和  |
C.6 +4 +4 和 和  | D.4( + + )和 )和  |
设 是两条直线,
是两条直线, 是两个平面,则
是两个平面,则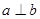 的一个充分条件是( )
的一个充分条件是( )
A.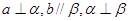 | B.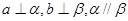 |
C.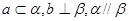 | D.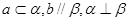 |
某四面体的三视图都为直角三角形,如图所示,则该四面体的体积是( )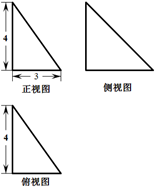
A. | B. | C. | D. |
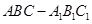 的主视图(又称正视图)是边长为4的正方形, 则此正三棱柱的侧视图(又称左视图)的面积为( )
的主视图(又称正视图)是边长为4的正方形, 则此正三棱柱的侧视图(又称左视图)的面积为( )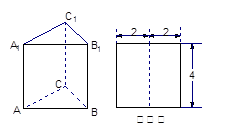
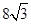


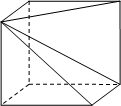




 内的射影构成的图形面积的取值范围是( )
内的射影构成的图形面积的取值范围是( )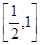

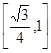
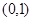
 ,则以该正方体各个面的中心为顶点的凸多面体的体积为 ( )
,则以该正方体各个面的中心为顶点的凸多面体的体积为 ( )