题目内容
定义在非零实数集上的函数f(x)满足f(xy)=f(x)+f(y),且f(x)在(0,+∞)上单调递增,则不等式f(
x)+f(x-5)≤0的解集为
| 1 | 6 |
[-1,0)∪(0,2]∪[3,5)∪(5,6]
[-1,0)∪(0,2]∪[3,5)∪(5,6]
.分析:首先判断出函数f(x)定义在非零实数集上的偶函数,再将抽象不等式利用函数单调性转化成具体不等式-1≤
x(x-5)≤1去解.
| 1 |
| 6 |
解答:解:在f(xy)=f(x)+f(y)中,
令x=y=1,得f(1)=2f(1),f(1)=0,
令x=y=-1,得f(1)=2f(-1),f(-1)=0
令y=-1,得f(-x)=f(x)+f(-1)=f(x),
函数f(x)定义在非零实数集上的 偶函数.
不等式f(
x)+f(x-5)≤0可以化为f[
x(x-5)]≤f(1 ),-1≤
x(x-5)≤1.,-6≤x(x-5)≤6.且x≠0,x-5≠0.
在坐标系内,如图函数y=x(x-5)图象与y=6,y=-6两直线.
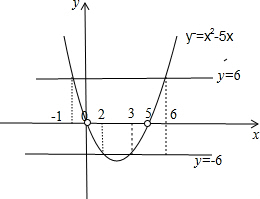
由图可得x∈[-1,0)∪(0,2]∪[3,5)∪(5,6]
故答案为:[-1,0)∪(0,2]∪[3,5)∪(5,6]
令x=y=1,得f(1)=2f(1),f(1)=0,
令x=y=-1,得f(1)=2f(-1),f(-1)=0
令y=-1,得f(-x)=f(x)+f(-1)=f(x),
函数f(x)定义在非零实数集上的 偶函数.
不等式f(
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 6 |
在坐标系内,如图函数y=x(x-5)图象与y=6,y=-6两直线.
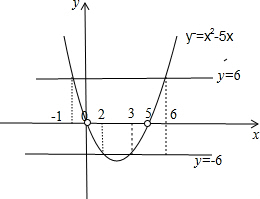
由图可得x∈[-1,0)∪(0,2]∪[3,5)∪(5,6]
故答案为:[-1,0)∪(0,2]∪[3,5)∪(5,6]
点评:本题考查抽象函数、不等式解.将抽象不等式利用函数单调性转化成具体不等式是关键步骤和解法的核心思想.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案
相关题目