题目内容
已知函数f（x）的反函数为g（x）=log2x+1，则f（2）+g（2）=
- A.1
- B.2
- C.3
- D.4
D
分析：根据互为反函数的两个函数之间的关系，即反函数的定义域是原函数的值域知，要求f（2），
只要在其反函数g（x）=log2x+1的解析式中，把g（x）换成2，求解x即可．
解答：由log2x+1=2得log2x=1，所以x=2，即f（2）=2，而g（2）=log22+1=2
所以f（2）+g（2）=2+2=4．
故选D．
点评：本题考查了函数及其反函数值的求法，考查了逆向思维，本题也可先求出f（x），因为两个函数互为反函数．
分析：根据互为反函数的两个函数之间的关系，即反函数的定义域是原函数的值域知，要求f（2），
只要在其反函数g（x）=log2x+1的解析式中，把g（x）换成2，求解x即可．
解答：由log2x+1=2得log2x=1，所以x=2，即f（2）=2，而g（2）=log22+1=2
所以f（2）+g（2）=2+2=4．
故选D．
点评：本题考查了函数及其反函数值的求法，考查了逆向思维，本题也可先求出f（x），因为两个函数互为反函数．
练习册系列答案
相关题目
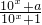是奇函数．
的反函数为f-1(x)=
(x≥0),则由函数f(x)=2
确定的数列{an}的反数列为{bn},求{bn}的通项公式;不等式
+
+…+
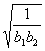≥1-2a对任意的正整数n恒成立,求实数a的范围;